Introduction to Population Genetics

Required readings:  Avise text, pp. 248-257, Gillespie book Chapters 1, 2 and 5.

Population genetics is the study of Mendel�s laws, the Hardy-Weinberg principle and other genetic principles as they apply to entire populations of organisms. Population genetics describes genetic variation in populations, and determines, by observation, experiment and theory, how that variation changes over time and space. In other words, how much variation exists in natural populations, and how can we explain variation in terms of origin, maintenance, and evolutionary importance?

What�s useful about population genetics?

• Management issues. We can answer questions about patterns and trends in genetic variability, gene flow (are populations genetically connected?), patterns of dispersal (do males or females tend to disperse further?), N_e (effective population size, which we will address below), fluctuations in population size (called "bottlenecks" and also addressed below), forensics applications (legal cases -- does the carcass in the suspect�s freezer match the poached animal found by a warden), and population size estimation (using genetic mark-recapture techniques).

• Conservation of threatened and endangered species. Assessment of genetic variability to prevent inbreeding depression (useful only for captive breeding programs aimed at highly valued, charismatic organisms such as black-footed ferrets), recognition of threatened and endangered species (is this candidate "species" actually distinct from a more widespread common form found elsewhere?), and molecular forensics for law enforcement (is this animal part from an endangered ferret or a legal mink?).
 
• Evolutionary understanding.  Population genetics provides a coherent framework for understanding how biodiversity is created and maintained.  Population genetics helps explain the spread of traits under the influence of natural selection (a huge topic, which I will largely ignore). 

The Hardy-Weinberg principle (and its predicted equilibrium) is the cornerstone of population genetics.  Developed independently by George Hardy and Wilhelm Weinberg in the early 1900�s, the Hardy-Weinberg principle is a model that relates allele frequencies to genotype frequencies. Like most models, Hardy-Weinberg is a simplification of real world complexities  -- but it has amazing explanatory power nonetheless.

Remember (memorize) the five major assumptions that lead to a Hardy-Weinberg equilibrium (click links to see discussion of each force):

• No Non-random Mating
• Infinite population size (= No Genetic Drift)
• No Mutation
• No Genetic Migration (permanent movement of alleles from one population to another, usually by dispersal of individuals)
• No Natural Selection (plus sexual selection)

Violations of any of the five major assumptions are the primary forces that drive evolutionary change.

Remember that an allele is a variant form of a gene (piece of DNA) at a single locus (Latin for "place", so we are referring to a particular stretch -- for example a stretch of 275 base pairs on Chromosome 13).  An allele frequency (geneticists call it "gene frequency") is therefore a measure of the commonness of an allele in a population (the proportion of a specific allele in a population -- how common is the A ["big A"] allele, or the a ["little a"] allele). A genotype is the specific allele composition for a certain locus or set of loci (Aa, AA, or AaBBcc for several loci vs. a second genotype AabbCc). Genotype frequency is a measure of the commonness of a genotype in a population; i.e., the proportion of a specific genotype in a population. Two major terms are important in discussing genotypes: homozygote and heterozygote. A homozygote has two copies of the same allele (e.g., AA or bb). A heterozygote has two different alleles at a given locus (e.g., Aa or Dd). Because the allele and genotype frequencies are proportions they always sum to 1.0, if we have included all the possible variants.

Allele frequencies:

p + q = 1                                                                                                Eqn 3.1

Expected genotype frequencies:

p² + 2pq + q² = 1                                                                                     Eqn 3.2

With the five assumptions given above, one can calculate the genotype frequencies for a gene with two alleles (A and a). The frequency of homozygous genotype AA is the probability of one allele A being in combination with another allele A. The expected frequency is simply the product of the separate allele frequencies. We will use the term p to refer to the frequency of allele A:

Frequency of aa = q²                                                                                 Eqn 3.5

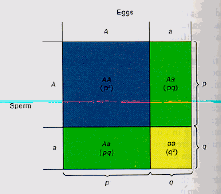
Fig. 3.1. Diagram of Hardy-Weinberg genotype proportions. Given a locus with two alleles designated A and a that occur with frequencies p and q, the chart shows the genotype frequencies (p², 2pq, and q²) as differently colored areas. Note that the heterozygotes (blue + yellow = green) can be formed in two different ways (in terms of combination theory, this means order is not important).  Extending this logic and its implications to multiple alleles and multiple loci provides the basis for much of the core theory of population genetics.

The expected frequency distribution of genotypes AA, Aa, and aa in proportions p², 2pq and q² respectively is called the Hardy-Weinberg equilibrium. If the population meets the eight assumptions listed above, then the population will go to the Hardy-Weinberg equilibrium in the first generation, and remain there. Again, the Hardy-Weinberg principle and its predicted equilibrium, is a simple model that serves as a starting point for examining the genetic structure of populations.

Violating Hardy-Weinberg assumptions

How likely are we to meet the major assumptions of random mating, no drift, no mutation, no migration, and no natural selection? If we violate the assumptions, how much difference does it make? Here is a list of processes that violate the Hardy-Weinberg assumptions and some discussion of each of them.  These "big five" forces are the major engines of evolutionary change. An important point is whether the given force tends to increase or decrease the genetic variability in populations.

• Non-random mating (tends to reduce genetic variation)

Random mating means that alleles (as carried by the gametes -- eggs or sperm) come together strictly in proportion to their frequencies in the population as a whole. Example: if p = 0.6 and q = 0.4, then the probability of an Aa heterozygote is 0.48 (the product of the allele frequencies, plus consideration of the fact that two ways exist to make a heterozygote; see Fig. 3.1). Situations where the random mating assumption does not hold include:

• Inbreeding � cases where relatives (e.g., siblings, cousins) have a greater probability of mating with each other than with other members of the population.
  Inbreeding will tend to decrease heterozygosity without affecting allele frequencies.
  
• Geographic structuring � in many cases individuals are more likely to mate with geographically proximate individuals than with more distant individuals.
  Geographic structuring is essentially an extended form of inbreeding.
  
• Positive/Negative Assortative mating � in positive assortative mating (usually called just assortative mating) individuals of a given phenotype or genotype tend to mate with similar individuals (e.g., A₁A₁ tend to mate with other A₁A₁).
Assortative mating will decrease heterozygosity (put like alleles together) without affecting gene frequencies.
In negative assortative mating (usually called disassortative mating) individuals tend to mate with dissimilar individuals.
Disassortative mating will tend to increase heterozygosity (put unlike alleles together) without affecting gene frequencies.
• Rare allele advantage.  In some mating systems a male bearing a rare allele will have a mating advantage.
  Rare allele advantage will tend to increase the frequency of the rare allele and hence increase heterozygosity.
  
• Mating system effects � in a polygynous mating system one or a few males that obtain a disproportionate share of the matings will be over-represented genetically (this differs from the rare allele effect mainly in that the male's success is not dependent on having rare alleles -- any rare alleles he does happen to have, however, will increase in frequency in the next generation).  Variance in mating success can change both gene frequencies and the level of heterozygosity (up or down will depend on the genotypes of the successful males relative to the frequencies in the population).

• Random genetic drift (always reduces genetic variation)

The effect of random genetic drift is inversely proportional to population size.  Allele frequencies change because the genes appearing in offspring are not a perfectly representative sampling of the parental genes (in a finite population). Since drift is a random process, outcomes of drift must be stated as probabilities. Drift removes genetic variation from the population at a rate inversely proportional to population size. As population size decreases the force of drift increases, and vice versa. Drift also affects the probability of survival of new mutations. The probability that an allele will move to fixation is equal to its frequency in the population -- an allele with a frequency of 0.2 (20%) has a 20% chance of fixation. New alleles introduced by mutation almost inevitably begin at low frequencies and have a low probability of fixation. Drift can lead to the loss of rare alleles and the fixation of common alleles. If the population is large, however, drift has little effect.

Marble analogy:  Think of a jar containing a million marbles in ten different colors. If we draw a random sample of 500,000 it will almost certainly contain all the marbles in proportions very similar to the original proportions. If we pick only five marbles, however, we will definitely have a biased sample (we can�t have picked more than 5 of the 10 alleles  -- any duplicates and we'll have even fewer alleles). Even if we take a sample of 50, we will be unlikely to maintain the proportions of the original million -- the small sample prevents us from drawing a representative array.  Similarly, drift is inversely proportional to population size -- large population = minor drift, small population = major drift.

Drift can have major effects on endangered (small, almost by definition) populations. For other species it can take a long time (thousands, hundreds of thousands or even millions of years) for drift to have large effects.

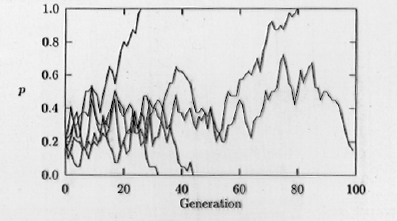
Fig. 3.2. Computer simulation of genetic drift. The fate of the A₁ allele (with frequency p, on the Y-axis) is shown in five replicate populations for a time course of 100 generations (time on the X-axis). Note that if p drops to 0 or rises to1.0 then A₁ will be lost (0) or reach fixation (1.0). Those frequencies (0 and 1.0) are therefore called "absorbing boundaries". Notice also the jagged trajectories that often characterize random processes.

• Selection (reduces genetic variation)

Selection is the differential survival and reproduction of phenotypes that are better suited to the environment or to obtaining mating success. Selection is the evolutionary force responsible for adaptation to the environment. Selection generally removes genetic variation from the population (occasionally special circumstance such as "frequency-dependent" or "balancing" selection can serve as forces maintaining variation). Alleles that confer advantages in survival or reproduction will tend to be represented in greater proportion in the next generation. After numerous generations (the time required will depend on the intensity of selection and the heritability of the trait), the advantageous allele will tend to spread to fixation. It is sometimes useful (and almost always interesting) to distinguish, as Darwin did, between natural and sexual selection.

If drift and natural selection tend to reduce genetic variation, what maintains or increases it? -- Mutation.

• Mutation (increases genetic variation and introduces novel variants)

Mutation is the process that produces a gene or chromosome set differing from the wild-type (ancestral allele). Mutation restores genetic variation to a population by producing novel alleles. Mutation is difficult to measure or observe directly, and rates of mutation can vary between loci. It is usually a weak force and therefore tends not to pull populations very far from Hardy-Weinberg equilibrium  -- over long enough time periods, though, even a weak force can have major effects (e.g., the erosion of the Grand Canyon).  Much of the neutral theory of genetic variation is based on a calculation of the balance between drift and mutation as forces of change.

• Genetic Migration (distributes and homogenizes genetic variation)

Genetic migration is the permanent movement of genes from one population into another. Migration can restore genetic variation into isolated and differentiated populations or reduce variation among populations when it occurs frequently. Assessing the patterns and importance of genetic migration (often referred to as "gene flow") is one of the major aims of population genetics. [Note that this definition of migration is very different from that for the seasonal back and forth movement of birds, for example, from breeding grounds in the temperate zone to non-breeding grounds in the tropics.  Migration, in that sense may have little effect on permanent movement of alleles]. 

Some absolute basics about probability and combination theory:

Much of population genetics involves manipulations of equations that have a base in either probability theory or combination theory.  We saw combination theory in action when we used the formula for the number of distinct unrooted trees as a function of the number of OTUs.  The basic Hardy-Weinberg equation p² + 2 pq + q² is a probabilistic one (with the addition that since order is unimportant we account for two ways to get heterozygotes).

Rule 1:  If you account for all possible events, the probabilities sum to 1.  [e.g., p + q = 1 for a two-allele system].

Rule 2: The probability that two independent events occur is the product of their individual probabilities.
        [e.g., probability of a homozygote is q*q = q²].

Punch line: Genetic techniques examine individual variation to discern the emergent properties of populations and higher taxa. We can examine genetic variation at multiple scales -- from the level of the individual (e.g., forensics applications) to analysis of higher taxa in systematic and taxonomic studies. Population genetics integrates a broad spectrum of process and pattern -- geneticists simplify by including only essential forces in their models and by making simplifying assumptions that, if violated, do not change the qualitative conclusions. A traditional first step is to build from the Hardy-Weinberg principle -- despite its admittedly unrealistic assumptions of random mating, no drift, no mutation, no migration, and no natural selection. In situations where one or more of these assumptions is clearly violated in a major way, a variety of more complex models can then be brought to bear on the problem.

Return to top of page