Lecture notes for ZOO 4400/5400 Population Ecology
Lecture 35 (21-Apr-06)
Return to Main Index page
Go back to notes for Lecture 34, 19-Apr
Go forward to lecture 36
24-Apr-06
Go to worked example for take-home exam
Go to Excel spreadsheet for calculating gene frequencies and local
inbreeding coefficient from genotypic counts
Population Genetics (continued)
Go to Glossary of genetic terms
Go
to worked FST calculation web page.
Violating Hardy-Weinberg assumptions (continued)
I ended the last lecture with a discussion of how non-random mating can produce genetic and evolutionary change. We will now examine
each of the other four forces of evolutionary change -- migration, mutation, drift and selection.
Genetic Migration (high gene flow maintains similarity among populations)
Genetic migration is the permanent movement of genes from one population into another. Migration can restore genetic variation into isolated and
differentiated populations or reduce variation among populations when it occurs frequently. Assessing the patterns and importance of genetic
migration (often referred to as "gene flow") is one of the major aims of population
genetics. High gene flow will tend to maintain genetic similarity among populations. For example, new alleles arising
by mutation in one population, will be carried to other populations by dispersing individuals.
Mutation (random source of new genetic variation)
Mutation is the random process that produces a gene or chromosome set differing from the wild-type (ancestral allele). Mutation restores
genetic variation to a population by producing novel alleles. Mutation is difficult to measure or observe directly, and rates of
mutation can vary between loci. It is usually a weak force and therefore tends not to pull populations
very far from Hardy-Weinberg equilibrium -- over long enough time periods, though, even a weak force can have major effects (e.g., the
erosion of the Grand Canyon). When populations are separated by geographic barriers, they will tend to develop independent
mutations and if enough different mutations occur, the populations will diverge enough to become distinct species.
Drift (a random genetic sampling process that can change allele frequencies and lead to fixation or loss of alleles)
Now we will turn to another random force -- genetic drift. Although it has a negligible effect in very large populations, genetic
drift can be a major force in changing gene frequencies in small populations. Random genetic drift is a change in allele
frequencies that occurs because the genes appearing in offspring are not a perfectly representative sampling
of the parental genes. Since drift is a random process, outcomes of drift
must be stated as probabilities. Drift removes genetic variation from the
population at a rate inversely proportional to population size. As population size decreases, the force of drift increases, and vice versa. Drift
also affects the probability of survival of new mutations. The probability that an allele will move to fixation is equal to its frequency in the
population -- an allele with a frequency of 0.2 (20%) has a 20% chance of fixation. New alleles introduced by mutation almost inevitably begin at low
frequencies and have a low probability of fixation. Drift can lead to the loss of rare alleles and the fixation of common alleles.
If the population is large, however, drift has little effect. Think of a jar containing a million marbles
in ten different colors. If we draw a random sample of a million (with replacement) it will almost certainly contain all the marbles in
proportions very similar to the original proportions. If we have only 20 marbles, however, and pick a sample of 20 with replacement, we are
quite mlikely to have some of the 10 colors missing, and some colors overrepresented.
Even if we sample with replacement from a population of 100, we will be unlikely to maintain the proportions of the original population --
similarly, drift is inversely proportional to population size -- large population, minor drift, small population, major drift. Drift can have major
effects on endangered (small almost by definition) species. For other species it can take a long time (thousands, hundreds of thousands or even millions
of years) for drift to have large effects.
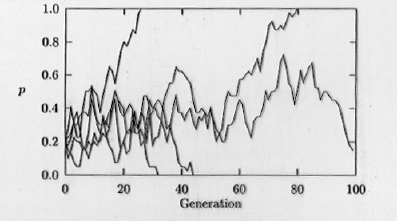
Fig. 35.1. Computer simulation of genetic drift acting within a small population (20 individuals). The fate of
the A allele (with starting frequencies of p = 0.2, on the Y-axis)
is shown in five replicate populations of 20 individuals, for a time course of 100 generations (time on the X-axis). Note that if
p drops to 0 or rises to 1.0 then A will be lost (0) or reach fixation (1.0). [Fixation means that all the individuals in a population have that allele -- i.e., no genetic variability exists at that locus in
that population]. Those frequencies (0 and 1.0) are therefore called "absorbing boundaries". Once the frequencies hit
either boundary they won't change (unless mutation adds another allele or "recreates" the lost
allele). Notice also the jagged trajectories that often characterize random processes.
Selection
Selection is the differential survival and reproduction of phenotypes that are better suited to the environment or to obtaining mating
success. Selection is the evolutionary force responsible for adaptation to the environment. Selection generally removes genetic variation
from the population (occasionally special circumstance such as
"frequency-dependent" or "balancing" selection can serve as forces maintaining variation).
Alleles that confer advantages in survival or reproduction will tend to be represented in greater proportion in the next generation.
After numerous generations (the time required will depend on the intensity of selection and the heritability
of the trait), the advantageous allele will tend to spread to fixation.
How the forces combine: Dodo as case history
Non-random mating, drift and selection tend to reduce genetic variation. What maintains it? -- Mutation.
For neutral genetic markers (not subject to selection) we will often be
interested in the balance between drift and mutation, and the level of gene flow
that prevents differentiation among populations. Small isolated populations
will tend to have no gene flow to connect them to related populations elsewhere.
Their mutations will increase or maintain genetic variation but those
mutations will be different from the mutations arising in the related populations.
Finally, the effects of drift will tend to randomly fix some alleles and
cause the loss of other alleles. The result can be fairly rapid evolution
of very different forms -- the Dodo (familiar to many from Alice in Wonderland)
was a very peculiar-looking flightless bird found on the island of Mauritius
(way off the island of Madagascar and highly isolated out there in the
Indian Ocean). The Dodo was driven to extinction by overharvest and the introduction of domestic animals in the late 17th century.
Recent genetic analyses confirm an earlier suspicion that the Dodo was an extremely divergent form of pigeon.
Drift, selection, mutation and low gene flow all combined to cause it to become something that few would recognize
as a relative of the familiar Rock Dove (city pigeon) or Mourning Dove.

Fig. 35.2. Artist's reconstruction of the Dodo, a large
(> turkey-sized), flightless bird of Mauritius (Indian Ocean), driven to
extinction in the late 17th century. Genetic analyses of dried tissue
from the one (partial) specimen in the British Museum indicate that the Dodo is a type of pigeon. Mutations, low gene flow, natural
selection, genetic drift and probably non-random mating likely all combined to cause
the extreme divergence that separates this unusual bird from its closest mainland relatives. Other, usually slightly less
dramatic, examples abound of the divergence of island populations from their mainland
progenitors. In the Rocky Mountain west mountain chains may act as "islands" of habitat, creating the conditions
for genetic divergence among populations on different mountain chains.
Punch line: Genetic techniques examine individual variation to discern
the emergent properties of populations and higher taxa. Genetic variation
can be used at multiple scales -- from the level of the individual
(e.g., forensics applications) to analysis of higher taxa in systematic and taxonomic
studies. Population genetics assesses a wide variety of processes and patterns
-- geneticists simplify their analyses by using models that incorporate
the essential forces and by using simplifying assumptions for which the impact of violations is either minor or at least does not change the
qualitative conclusions drawn. A traditional first step is to use the Hardy-Weinberg
principle -- with its admittedly unrealistic assumptions of random mating, no drift, no mutation, no migration, and no natural selection. In
situations where one or more of these assumptions is clearly violated in a major way,
a variety of more complex models can then be brought to bear on the problem.
Measuring genetic variation in natural populations -- Heterozygosity (or gene diversity)
When we actually go out to assess genetic variability in natural populations,
some of the first and most important measures we take are the observed and expected heterozygosities. These tell us how much
variation exists in the population and how that variation is distributed across the alleles in the loci we are examining.
Heterozygosity is of major interest to students of genetic variation in natural populations. It is often one of the first
"parameters" that one presents in a data set. It can tell us a great
deal about the structure and even history of a population. Just for example, very low heterozygosities for allozyme loci in cheetahs and
black-footed ferrets indicate severe effects of small population sizes (population bottlenecks
or metapopulation dynamics that severely reduced the level of genetic variation relative to that expected or found in comparable mammals).
Several measures of heterozygosity exist. We will focus primarily on expected heterozygosity (HE, also
written as Hexp and termed gene diversity by population geneticist Bruce Weir). The simplest way to calculate it for
a single locus is as:
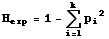 Eqn 35.1
Eqn 35.1
where pi is the frequency of the ith
of k alleles. [Note that p1, p2,p3
etc. may correspond to what you would normally think of as p, q, r, s
etc.]. If we want the expected heterozygosity over several loci we need double summation and subscripting as follows:
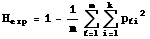 Eqn 35.2
Eqn 35.2
where the first summation is for the lth
("ellth") of m loci. [Note that we average over the m loci via the 1/m term].
Expected heterozygosity is equal to one minus the expected homozygosity.
Why does it work to take the sum of the squared gene frequencies and subtract that from one? Let's think back to basic Hardy-Weinberg:
p2 + 2 pq + q2 = 1
where the heterozygosity is given by 2pq. The rest of the expression (p2 + q2)
is the homozygosity. If we want the heterozygosity we just subtract that from the total. With just two alleles it isn't as efficient to
calculate the heterozygosity by the "one minus the homozygosity route". Consider the case, though, of a locus with 6 alleles.
It has 21 possible genotypes -- 6 kinds of homozygotes and 15 kinds of heterozygotes.
The number of possible combinations is given as the sum of all the numbers from one to the number of alleles, which has a simple formula:
6 + 5 + 4 + 3 + 2 + 1 = 21 = [6*(6+1)]/2
or more generally
 Eqn 35.3
Eqn 35.3
this summation formula is also the way to calculate the number of combinations of y things taken two at a time
(where order is unimportant ). In terms of our allelic notation, the number of possible genotypes is:
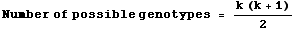 Eqn 35.4
Eqn 35.4
For k > 3 it's much simpler to simply
square
the k different gene frequencies and sum them than it would be
to
enumerate and calculate the many different heterozygote
frequencies.
We trade a little inefficiency on two-allele systems for much greater
efficiency
with multi-allele systems.
Heterozygosity is maximal when the allele
frequencies
are equal. What does heterozygosity
tell us and what patterns emerge as we go to multi-allelic systems?
Let's
take an example. Say p = q = 0.5. The expected
heterozygosity,
Hexp,
for a two-allele system is described by a concave down parabola that
starts
at zero (when p = 0) goes to a maximum at p = 0.5 and
goes
back to zero when p = 1.
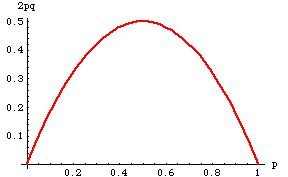
Fig. 35.3. Expected heterozygosity (Hexp
= 2pq) for a 2-allele system as a function of allele frequency, p.
Note that the heterozygosity peaks at a value of 0.5, when the allele
frequencies
are equal (p=q). It is minimal at both extremes --
in those cases everyone is a homozygote of one type or the other.
In fact, for any multi-allelic system,
heterozygosity,
Hexp,
is greatest when
p1 = p2
= p3 = ….pk
that is, when the allele frequencies are equal. For
example, the maximum heterozygosity for a 10-allele system comes when
each
allele has a frequency of 0.1. Hexp then
equals 0.9.
Individual’s-eye view of
heterozygosity
(Hexp = probability that an individual will be
heterozygous)
Here is a way that I like to think of
heterozygosity
(Hexp ). It is the (expected) probability that an
individual
will be heterozygous at a given locus (or over the assayed loci for a
multi-locus
system). For many human microsatellite loci, for example, Hexp
is often > 0.85, meaning that you have a > 85% chance of being a
heterozygote.
From heterozygosity to F-statistics:
a way of assessing genetic differences among populations.
Heterozygosity is one of the best ways to
approach
the analysis of differences among populations. We will use
heterozygosities
as the basis for calculating something called F-statistics. F-statistics
are a general statistical tool for analyzing variances (variation in
gene
frequencies). They are not restricted to genetic
applications.
In the 1930's, however, Sewall Wright of the University of Chicago,
pioneered
their application to genetic studies of natural populations. With
the rise of genetic laboratory techniques such as allozymes in the
'60's
and '70's, F-statistics became one of the fundamental tools of
population
genetics applied to natural populations.
Local (per subpopulation) F, with no
subscript
(or just one to denote the subpopulation):
Within a subpopulation, we can
calculate the unsubscripted statistic, F, as the ratio of (the
difference
between expected and observed heterozygosity) to (expected
heterozygosity).
The general formula is:
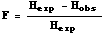 Eqn 35.5
Eqn 35.5
where Hexp is given by Eqn 35.1
or 35.2, and Hobs is the observed proportion of
heterozygotes.
Global (over a set of subpopulations) F-statistics,
with two subscripts:
For a set of subpopulations for
which we have genotypic information, we usually consider F-statistics
to have three levels, each named by a different set of
subscripts.
These reflect three levels of biological organization, Individuals,
Subpopulations,
and the Total population (a set of
>= 2 subpopulations). We can assess heterozygosities at each
of these
levels and use them as the building blocks for creating levels of F-statistics.
Here are the three levels. The first two are the most important:
FIS
is
sometimes called the inbreeding coefficient, It assesses
global
variation in Individuals, relative to the variation in their Subpopulation.
If FIS is negative, then the set of
subpopulations,
as a whole, is outbred (has an excess of heterozygotes).
If FIS is positive then the set of
subpopulations,
as a whole, is inbred (deficiency of heterozygotes).
FST
is
probably the most important. It assesses the variation in the Subpopulations
relative to that in the Total population.
It can have values between 0 and 1.0 (i.e., it cannot be negative).
FST
of zero means that all the subpopulations have the same gene
frequencies.
FST
of 1.0 means that the subpopulations have completely nonoverlapping
sets
of alleles (the subpopulations are fixed for different alleles).
Natural populations tend to have FST values that
range
between near zero up to just greater than 0.5.
Values of FST above approximately 0.2 are considered
"high".
FIT is
relatively
rarely used. It assesses the variation in Individuals
relative
to the variation in the Total set of subpopulations.
In general, F-statistics can range from
values
of -1 to +1. As we saw above, FST has a more
restricted
ranges of possible values (0 to 1).
To calculate the F-statistics above we
use
three kinds of heterozygosity values.
HI
is the average observed heterozygosity in individuals.
HS
is the expected heterozygosity (gene diversity) of
subpopulations,
calculated as the weighted average across a set of subpopulations.
We use Eqn 35.1 to calculate the expected heterozygosity in each
subpopulation,
then weigh the results by the subpopulation sizes
HT
is the expected heterozygosity over the whole set of populations.
We use the global gene (allele) frequencies and then plug them in to
Eqn 35.2 to calculate it.
I have set up a complete worked example of
calculating
gene frequencies, observed versus HWE expected genotypic counts,
heterozygosities,
and F-statistics on a separate web page. The example is a
two-allele, three population case. You will calculate the same
sets
of statistics for a three-allele, four-population case in Homework 8.
Go
to worked FST calculation web page.
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Return to top of page
Go forward to lecture 36
, 24-Apr-06


