Lecture
notes for ZOO 4400/5400 Population Ecology
Lecture 27 (8-Apr-13) Population regulation --
density-dependence vs. density-independence
Return
to Main Index page Go
back to notes for Lecture 26, 1 and 3-Apr-13 Go
forward to lecture 28 8-Apr-13
We now turn to something that
has been an implied theme throughout -- population
regulation. We began the course with the exponential model for unchecked
growth in the absence of any other forces, but then very quickly added
one regulating force -- the density-dependent "crowding effect" of the logistic
growth model. Let's develop a list of a number of factors that
can help keep populations in check (regulate their numbers) and then
adapt the model we used for harvest to look at the interplay between two
major kinds of potential regulating factors -- density-dependent factors and
density independent factors.
What are some potential regulating mechanisms?
Density-independent factors (possibly
more influential in insect dynamics? Likely to be more important
for species that can grow so quickly they do not function very well as
self-regulators):
Weather (storms, cold, drought)
Density-independent diseases (probability of occurrence does not change
with density; human example = cancer)
Density-dependent (possibly
more influential in vertebrate dynamics?):
Food
Space (territories, denning sites, nest cavities)
Density-dependent epizootics (disease epidemics;
transmission/infection likelihood changes with population density --
human example = measles, SARS)
How do we figure out which factor matter?
Experiments may be useful. Often factors overlap, so that it is hard to tell whether
a factor is really regulatory. Consider the concept of compensatory vs.
additive mortality. Applied managers will usually consider hunting
harvest to be largely compensatory ("animals would have died anyway"); basic
(meaning studying a problem for its own sake, as opposed to applied)
biologists will often consider any source of mortality they measure as being
additive.
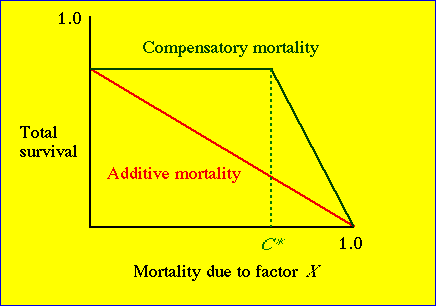
Fig. 27.1. Distinction between
additive and compensatory mortality. If a given mortality factor (Factor
X, such as harvest, poisoning or predation) causes an immediate reduction
in total survival, it is considered an additive mortality factor.
A compensatory factor, in contrast, causes no reduction in
total survival (until it reaches some threshold value, C*).
Along the horizontal portion of the compensatory mortality line, animals
dying from the compensatory factor would have died anyway of some other cause.
Consider the implications of compensatory mortality. In a harvest management
context, compensatory mortality may be a "good thing" -- we can harvest
a reasonable proportion of the population without increasing total mortality
(anywhere up to the C* "threshold" point in Fig. 27.1).
In a pest management program, however, it will be disheartening if high levels of
mortality achieved with great effort and expense are all simply
compensatory. The same may be true of some "predator control" programs for species
such as coyotes that have fairly high potential reproductive rates.
Compensatory mortality can make it difficult to discern the factor that truly regulates
a population. A compensatory factor may be sufficient to regulate
a population but it may not be necessary (some other factor could,
and will, take its place). Look back at notes for Lecture 3, to
brush up on necessary vs. sufficient conditions.
Two arguments against density-independence (after A. J. Nicholson.
1933, Australian biologist famous for his work on lab. populations of blowflies):
Analogy to ocean: Nicholson argued that the size
of a population is analogous to the depth of ocean. The effects of weather
on populations would be analogous to the effects on the surface level of
the ocean by wind and tide -- the surface change may be driven by wind
or tide, but one would never attribute the cause of total ocean depth variation
to wind or tide -- likewise, other factors largely control population
size.
Destructive force vs. real control: even if weather
has huge effect on population size, it may not be the controlling factor.
Imagine a population of insects with a potential l
of 100 (100-fold potential increase per season -- or 100 females per mother
if we return to the concept of female demographic dominance). Weather destroys
98% of the individuals each season. That still allows the population to
double each season -- universe fills up. Now add a predator that responds
in a density-dependent manner to remove the "surplus" (1%) from the remainder
of the population. That predator (with its density-dependent
response) is
the controlling factor, even though numerically it destroys only a
small fraction of the population.
One of the themes we have dealt with repeatedly recently
is the stability of systems. Below, I combine the concepts of
density-dependence (largely based on biotic
interactions with internal feedbacks),
density-independence (largely due to environmental
stochasticity, particularly in weather)
and the stability or instability of
systems.
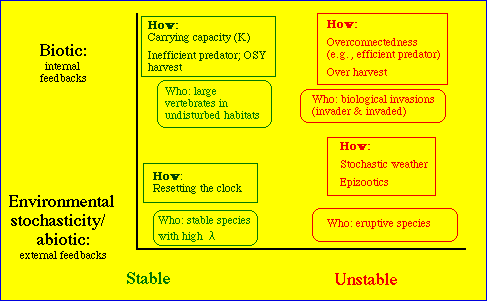
Fig. 27.2. A diagram to illustrate
some potential
interactions between density-dependence and density-independence (above
or below on the Y-axis) and stability or instability (on the X-axis).
The boxes list a few potential mechanisms (the "hows") and kinds of organisms
(the "whos") that might fall in each of the category combinations. "Resetting
the clock" means that just as a high-l
species is about to explode or irrupt, its numbers are set back by some
environmental or abiotic factor (such as cold or drought). Many arctic
or temperate invertebrate populations may have these sorts of dynamics
-- high growth potential that is checked by the end of the growing
season.
Of course, many natural populations will
occur in intermediate locations in the state space of the graph above, or they will
periodically experience effects that differ from the norm (e.g., relatively brief
non-equilibrium "crashes" following an unusually severe winter or reaction to the
invasion of a new and destabilizing competitor or predator). Further, many
natural populations (and the factors that affect them) will be " density vague"
meaning that the scatter of points around the relationship between any
particular factor and population size will be high enough that it will
be difficult to demonstrate unequivocal cause-and-effect relationships.
Nevertheless,
knowing the range of possible outcomes from the range of simple (at
least
compared to the complexity of the natural world) models can help us to
narrow the choices and think critically about the most likely factors
in
the wide range of contexts that face any biologist or manager.
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Return to top of page
Go
forward to lecture 28 8-Apr-13

