Lecture
notes for ZOO 4400/5400 Population Ecology
Lecture 31 (17-Apr-13) Experiments on population regulation; disease models
Required readings (PDFs on WyoWeb):
Hudson, P.J., A.P. Dobson, and D. Newborn. 1998. Prevention of population cycles by parasite removal. Science 282: 2256-2258.
Korpimäki, E., and K. Norrdahl. 1998. Ecology 79: 2448-2455.
May, R.M. 1999. Crash tests for real. Nature 398: 371-372.
Return to Main Index page Go back to notes for Lecture 30,
14-Apr Go forward to Lecture 32,
19-Apr-13
I will wrap up the section on population
regulation
with two experimental approaches that serve as useful case
histories.
Then I will introduce a brief section on using a clever solution of
first-order
difference equations to look at disease transmission. With the
recent
attention to chronic wasting disease (CWD), sometimes referred to as
"mad
elk" disease, and the problems related to brucellosis transmission
between
bison and cattle in Yellowstone, the population ecology of disease
spread
is clearly relevant.
Predator-prey cycles -- voles
and
a multi-species assemblage of avian and mammalian predators.
What factors drive the well known population
cycles
in voles? From the paper we read earlier by Turchin
et al. (2001) we know that the data are consistent with the
hypothesis
that vole cycle are driven by their predators. That is, the vole
dynamics are like those of prey in predator-prey models (their cycles
have
blunt peaks). Korpimäki and Norrdahl
(1998)
conducted a large-scale experimental reduction of predators. The
voles had four kinds of predators -- least weasels, Mustela nivalis,
stoats, M. erminea, Eurasian kestrels, Falco tinnunculus,
and Tengmalm's owl, Aegolius funereus. Their major
results
were as follows: 1) predator removal did reduce the cycling; 2)
it took removal of
all the predators to eliminate the cycling --
areas where only one or two of the four predators were reduced still
showed
prey cycling.
Some questions for you to consider by looking at
the Korpimäki and Norrdahl (1998) paper
directly
1) Describe at least two improvements of
this
study over previous attempts to assess the importance of predator-prey
dynamics as a causal factor in rodent population cycles.
2) What factors were important in choosing control
areas for comparison to experimental treatment areas?
3) How did the authors assess the pre- and
post-treatment
densities of the mammalian predators?
4) How did the authors reduce the density of avian
predators?
5) What is the importance of the first sentence
of the Discussion section of the paper?
6) Reduction of just the least weasel did not
prevent
the low point in the vole cycle. What factors do the authors
invoke
to explain why reduction of all the predators might be necessary to
preventing
cycling?
Red grouse and parasites. Hudson
et al. (1999) studied a classic cyclic population with boom-bust
cycles
-- the red grouse, Lagopus lagopus (same species that we call
Willow
Ptarmigan in the U.S.). The grouse had been broadly acknowledged
to undergo density-dependent regulation with time delays. The key
regulating factor, however, was undetermined. Candidate factors
included
the food supply (heather and willow), vertebrate predators, parasite
infestations,
territorial regulation or some other factor. Hudson et al.
discovered
that a parasitic nematode (helminthic gut worm) was the likely
agent.
Using host-parasite models (more sophisticated versions of the
predator-prey
models we studied earlier) they made predictions for six populations
for
which they predicted population lows (of the grouse) in 1989 and
1993.
They conducted an experiment in which they treated populations with
antihelminthics
(a medicine that kills the gut worms). Two populations received
full
treatments before each of the predicted lows. Two populations
were
treated only before the 1989 crash. The last two populations were
untreated controls. The results dramatically verified the
parasite
prediction. The untreated populations crashed to one tenth
of one percent of pre-crash population sizes. One of the two
doubly
treated treated populations remained steady through the predicted 1989
and 1993 crashes. The other doubly treated population decreased
to
a third of its pre-crash size. One of the two populations treated
only in 1989 remained steady in that year but underwent a major crash
in
1993. The remaining population underwent a tenfold reduction in
1989
and a major crash in 1993. Interestingly, the population with the
tenfold crash in 1989 probably received the lowest percentage of bird
treatments
(approximately 15%). Host-parasite models suggest a threshold for
vaccinations -- only when a certain proportion of the population is
vaccinated
will epidemics move from cyclic boom-bust outbreaks to lower steady
levels.
Hudson et al. estimated that the threshold required to dampen the
cycles
was approximately 20%. Again, as in the case of the Isle Royale
wolves
and moose, the "exception proved the rule".
A commentary on the vole and red grouse papers
was
the subject of a Nature "News & Views" article called "Crash tests
for real" by May (1999). That should be a useful guide to
studying
the results from theses two papers.
Bottom line --
focus
on nature and strength of interactions among populations.
As suggested by the above example, and the earlier assigned paper by Turchin et al. (2000) on vole and lemming cycles, interactions within and
between
trophic levels can be complex. Often, the question may not be one
of top-down or bottom-up regulation. Instead, it may be a matter
of the relative strength of interactions (or as in the McQueen
pike-bluegill-zooplankton-phytoplankton
study, a combination of effects from the top meeting effects from the
bottom)
. In some communities, the distribution of interaction strengths
may be highly skewed. A few population links may have very strong
interaction effects, while the great majority of interactions between
populations
are weak. In those sorts of communities it may be appropriate to
talk of keystone species.
Using first-order difference
equations
to examine the spread of infectious diseases.
Disease is probably a much more important
density-dependent
regulator of populations than was previously thought. Recent
examples
of wildlife diseases that have made the news have been brucellosis
(controversial
for bison and cattle in the greater Yellowstone area), chronic wasting
disease (CWD), with its focus in Colorado and Wyoming, and West Nile
virus,
which could be much more of a presence in Wyoming this summer.
Many diseases spread in ways that are susceptible
to modeling in forms that are somewhat similar to various other models
of population dynamics. We will use a fairly simple difference
equation model to make inferences about various population-level aspects of the
spread and equilibrium infection rates of an infectious disease.
The model itself was developed in the context of sociology -- to assess
the "mobilization" of voters to political parties (the cynical might
say
that such a process is disease-like). I adapted
this
from a formulation in Huckfeldt et al., 1993. As in many
of our modeling approaches, we will ignore many complications of the
real
world in order to focus in on a few key processes that we assume are
critical
to the process we seek to understand.
Inferences about first-order difference
equations
(building from an equilibrium/local stability analysis approach).
Here's the starting equation for the change in the
level
of infection:
 Eqn 31.1
Eqn 31.1
where It is the proportion of infected individuals at time t,
g is the probability of becoming infected per unit of time (say a year),
L is an upper limit on the proportion of the population that is susceptible, because some individuals
are immune (for whatever reason),
and r is the probability of recovering, if infected.
Note that the left hand side (LHS), It+1 - It , is the same thing as the "change in It ."
Rearranging this to be in recurrence form (meaning the
value
of some variable at time t+1, as a function of the value of
that
variable at time t) we get
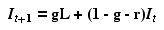 Eqn 31.2
Eqn 31.2
[All we did was move It to the RHS and factor out all the terms in It].
Note that Eqn 31.2 is in the form
Y = b +
mX
Eqn 31.3
where b is the Y-intercept and m
is the slope of a standard linear regression equation. Thus
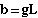 {Y-intercept}
Eqn 31.4
{Y-intercept}
Eqn 31.4
and m = (1 - g - r)
{slope}
Eqn 31.5
Now let's set the left hand side of Eqn 31.1 to zero
to get an equilibrium point and solve for It.
 Eqn 31.6
Eqn 31.6
 Eqn 31.7
Eqn 31.7
and finally to the equilibrium value of It, which we
will call I*
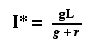 Eqn 31.8
Eqn 31.8
References:
Huckfeldt,
R.R., C.W. Kohfeld, and T.W. Likens. 1993. Dynamic Modeling: An
Introduction. Quant. Applic. Soc. Sciences No. 27.
Sage University Press, Thousand Oaks, CA
Hudson, P.J., A.P. Dobson, and D. Newborn. 1998. Prevention of population
cycles by parasite removal. Science 282: 2256-2258.
Korpimäki, E., and K. Norrdahl. 1998. Ecology 79: 2448-2455.
May, R.M. 1999. Crash tests for real. Nature 398: 371-372.
Turchin, P., L. Oksanen, P. Ekerholm, T. Oksanen, and H. Henttonen. 2000. Are
lemmings prey or predators? Nature 405: 562-565.
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Return to top of page
Go
forward to Lecture 32, 19-Apr-13
![]() Eqn 31.1
Eqn 31.1