The value of models and experimental approaches, the nature of pseudoscience

Return to Main Index page        Go back to notes for Lecture 2, 16-Jan    Go forward to notes for Lecture 4, 23-Jan

 Necessary and sufficient conditions  -- the best kind of explanation

In ecology and evolution, we are often interested in the conditions that cause a particular phenomenon to occur.   The most satisfactory explanations are those that describe conditions that are individually necessary AND jointly sufficient. Let's think about what that means.  If a condition is necessary, the phenomenon cannot occur without it.  We seek a set of necessary conditions each of which (the "individually" part) is necessary.  Failure to include any one of the necessary conditions would mean the phenomenon would not occur.  If a set of conditions (usually more than one) are sufficient, the phenomenon will occur whenever those conditions exist (regardless of other conditions).  We seek a set of conditions that, taken together (the "jointly" part) are enough to cause the phenomenon to occur without requiring any additional conditions.  Some conditions are necessary but not sufficient -- that implies incompleteness.  Other forces are required in order to explain the occurrence of the phenomenon.  Some conditions are sufficient but not necessary -- in that case our explanation is only one of several possible pathways by which the phenomenon can occur.  A complete description would describe the set of conditions that is both necessary and sufficient.  Perhaps the easiest way to think of conditions that are both necessary and sufficient is to think of two (or more) conditions that are necessary.  Neither alone is sufficient; both are necessary; together they form the necessary and sufficient conditions. Remember that we are interested in conditions that are necessary and sufficient to cause a particular consequence. For example, even if we find the necessary and sufficient conditions for rearing stocked trout to harvestable size, those conditions (suitable lake, appropriate water temperature and ample food) may not be sufficient to allow a self-sustaining population (the lake may lack the necessary spawning habitat).  What makes for a really powerful study?  Strong (likely experimental) evidence that you have found the necessary (all the listed conditions are needed) and sufficient conditions (given all those necessary conditions, the particular consequence will occur) to explain some ecological pattern.  Quite often, it turns out that some alternative set of conditions could also suffice (the Kaibab case would be the unconsidered alternative hypothesis of the change in sheep grazing). 

[Optional extra: check the website at: http://www.sfu.ca/philosophy/swartz/conditions1.htm  for a useful and more complete explanation of necessary and sufficient].

Observations can simplify by focusing on critical components and highlighting similarities and differences among phenomena (comparisons among taxa or systems).
Modeling simplifies by exposing the effects of a few model parameters, ignoring many or most of the complexities of the real world.
Experiment simplifies by holding all but a few factors constant (by the use of replicates and controls).

Last time I gave an example of uncritical acceptance of a plausible explanation (the Kaibab mule deer), and then outlined some ways to go about science with a higher degree of critical thinking.  Today, I consider the use of models and experiment in science in general and population ecology in particular.  I will then throw out some thoughts on how you might approach the learning process in this course and elsewhere.

Some different approaches to logical inference:

Strong inference (Platt, 1964): set up hypotheses and look for rejection so as to move forward to a new level of sophistication (ratchet or tree-climbing analogy)

Bayesian/likelihood approaches (see references in the next lecture/web page):
      The degree to which the data fit the hypothesis producing a
      Degree of belief in each of several alternative hypotheses.
      We can use prior information and conditional probabilities (prior probability ) as a tool in the evaluation of evidence
      The Bayesian philosophy extends to the mechanics of how one assesses statistical significance and is a
          controversial alternative to
          Classical statistics (rejection of a single null hypothesis): H_o = No difference between the means

  How well do models fit the data? Akaike Information Criterion allows us to compare the fit of alternative models to our real-life data. Anderson et al. 2000.

Romesburg (1981) argued that three main scientific methods/Types of Reasoning exist:
    1) Induction (see previous lecture)
    2) Retroduction (overused in wildlife management): a hypothesis that would explain a phenomenon if it were true (but that does not consider alternative hypotheses and has not been critically tested).  The glib acceptance of the predator control hypothesis for the Kaibab deer crash is a classic example of retroduction.
    3) Hypothetico-deduction (+ EXPERIMENT) underused in wildlife management. On the one hand, if Hypothesis A is true then it leads to predicted outcome X. On the other hand, if Hypothesis C is true, then it leads to predicted Y. If we set up an experiment (perhaps even one that would seem to favor Outcome X) and we get Outcome Y, then we have the basis for rejecting Hypothesis A.

Why use models or mathematical approaches?

1) To expose faulty assumptions, Gotelli uses exponential growth as an example. The assumption there is that growth is independent of population size/density. Seeing that the model almost never applies to natural populations (except for a short time following introductions or invasions) we are forced to incorporate density dependence, leading to the logistic equation.  

2)  To provide testable consequences or qualitatively new insights. 

Here's an example of one way we might use a model to gain insights that would be difficult to obtain in any other way. Later in the course we will see how logistic growth in a harvest function can intersect with logistic population growth to produce TWO equilibrium points (population sizes to which a harvested population will tend to return if they go above or below the equilibrium value).  The point here is not the particular example, rather it is to illustrate the very general point that models can guide our thinking, provide the basis for critical tests or experiments and clarify our thinking about a problem.
 

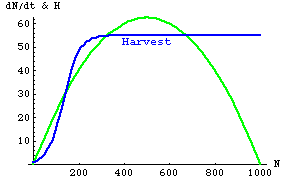
Figure 3.1. A model that explains a potentially puzzling population phenomenon.  Under certain conditions of harvest, a population that drops below a certain critical point will remain at a new lower equilibrium population size.  The blue s-shaped curve is harvest (animals removed), while the green humped curve is logistic population growth (animals added as a function of population size).  The system has three equilibrium points -- the places where the curves intersect.  The highest equilibrium point (at about N = 700) is stable (if the population goes a little above or below that point it will tend to return to that point).  The middle equilibrium point is unstable (above that the population will tend to increase, below it, it will tend to decrease).  Finally the smallest equilibrium point is also stable.  If the population goes below the unstable equilibrium point, it will tend to stabilize at a new, lower equilibrium point.  That might puzzle a management biologist unless she remembered the modeled example from her course in Population Ecology. 

Punch line: The insights (bold red highlight above) we gain from mathematical relationships such as the one shown above are not accessible by any other route.
The primary reason I have provided the graph above is NOT to make a particular point about harvest.
It IS to make a general point about how mathematical (and graphical) reasoning can lead to insights that would be very difficult to obtain by any other means.

Why use experimental approaches?

1) To control possible confounding factors (Correlation does NOT EQUAL causation) by randomization of possible confounding
        factors we want to be able to vary one possible causal factor at a time and assess its effect

2) To allow clear rejection of a plausible alternative hypothesis

Types of experiments in ecology

            Manipulative field    +  Very relevant to nature,
                       -  Difficult to conduct at meaningful scale,
                                                   difficult and expensive to control confounding variables,
                                                   and difficult to achieve meaningful replication

            Natural               +   Nature can treat large areas at no cost   (e.g. burned and unburned areas)
                        -  No control of confounding variables, not randomized (e.g.,fire).

But… we obviously can't conduct a controlled experiment on the Kaibab plateau mule deer population. We are left with no choice but to keep several alternative working hypotheses and look for evidence that changes the balance of likelihood towards one of those alternatives. Quinn and Dunham (1983) discuss the problem of multiple causation in ecology.

Later in the course we will examine in some detail several examples of moderate to large-scale ecological experiments

How songbirds keep down herbivores in forests (exclusion of birds by netting leads to reduced tree growth): Marquis and Whelan, 1994
How parasites help drive population cycles in red grouse (= ptarmigan).   Hudson et al., 1998
How predators drive population cycles of voles (reducing predators eliminated cycling pattern). Korpimaki et al., 1998

Student responsibility for the scientific method material:

       Know the basic steps in the scientific method, be able to discuss them, and illustrate with an example.

       Questions to ponder

What determines the usefulness of a hypothesis?
What constitutes "proof" of a hypothesis?
What is a fact?
Where do insight and intuition enter into the scientific method?
Where do the processes of induction, retroduction and deduction enter into the process?
How can we obtain knowledge?

[Much of the material from here to the end of the web page is material I will not cover in lecture, but do expect you to know]

Pseudoscience:

It's always easy to find a few flaws or apparent inconsistencies in any scientific argument. To challenge a theory (such as evolution) with a counter-argument that is SCIENTIFIC, however, you have to have an argument that is plausible, subject to test or evaluation of likelihood.  (We can never say for sure that the Martians didn't do it, we just consider it so unlikely, implausible and inconsistent with the rest of the evidence that we no longer consider it seriously as a scientific argument -- of course if you want to believe that the Martians did it, that's your prerogative).

"Scientific" creationism (now often camouflaged by the misleading term "intelligent design") is almost entirely rearguard pseudoscience to nip at the heels of scientific controversies in such a way as to make it look as though everything is confused (it's not at all confused it's simply dynamic and subject to scrutiny, which is entirely different).  The "scientific" creationists look for any disagreements between evolutionists and thereby conclude "our view is equally valid as science."
                IT IS NOT.
Anyone is (and should be) free to believe what they wish, including literal acceptance of a particular faith's interpretation of the Bible or other religious texts.  Nevertheless, the argument that those beliefs constitute science is not valid.  Scientific theories are subject to test, falsification and modification.  Beliefs are not subject to these constraints. Another popular argument recently has been that biological phenomena (e.g., the eye) are too complicated to be explained by a mechanistic theory of evolution.  In that respect, it is perhaps instructive to consider the history of Newtonian mechanics/physics.  When Newton and others developed their theories, many argued that the laws might explain the movements of the planets but that the complexities of forces operating on the surface of planet Earth (e.g., the weather) was such that they could only be explained by divine guidance. Even among the most devout creationists few today would try to argue that we must resort to explanations based on divine intervention in order to explain the physics of weather patterns or turbulent flow. Personally, I would be very hard pressed to explain the physics of how the earth revolves around the sun -- does that mean that I accept the more intuitively pleasing idea that the sun revolves around the earth? No. I accept the idea that the Earth circles the sun as a fact.  I accept the careful, skeptical, methodical work of those who seek to explain (with theories), the fact of a heliocentric (sun-centered) universe. 

Grad. students need to evaluate two of the following:
        either
               two readings from the list on scientific method (one of which should be the Anderson et al. 2000 paper)
        OR
Dennis, 1996 (anti-Bayesian) and one of the "pro"-Bayesian readings.

References on the scientific method

Andrewartha, S.G. 1961. Introduction to the study of animal populations. Mathuen: London. 218 pp. Chapter 9.33. The place of the model, the hypothesis, the null hypothesis, the experiment and the theory in scientific method. Pp. 118-183.
Bunge, M. 1967. Scientific Research I: The Search for System. Springer-Verlag New York, Inc., New York, N.Y.
Burke, J. 1985. The day the universe changed. Little Brown & Comp. Boston Mass.
Chamberlain, T.C. 1890. The method of multiple working hypothesis. Science 15:92.
     [This classic has been reprinted in numerous places, including the Hilborn and Mangel book listed below]
Dewey, J. 1938. Logic - the theory of inquiry. Holt and Co., N.Y. 546 pp. Chapter 21. Scientific Method: Introduction and deduction. Pp. 419-441.
Fretwell, S.D. 1972. Populations in a Seasonal Environment. Princeton Univ. Press, Princeton. Ch. 1.
        (pp. x-xix in Suggested Readings folder on WyoWeb)
Hilborn, R., and M. Mangel. 1997. The Ecological Detective: Confronting Models with Data. Princeton Univ. Press. Ch. 1.
Kuhn, T.S. 1970. The Structure of Scientific Revolutions, 2nd ed. Univ. of Chicago Press.
        [idea of paradigms governing "normal science" and the "revolutions" that overturn the paradigm]
Platt, J.R. 1964. Strong inference. Science 146:347-352.
Popper, K.R. 1959. The logic of scientific discovery. Hutchinson and Co., LTD., London. 480 pp. Chapter 1. A survey of fundamental problems. Pp. 27-48.
Quinn, J.F. and A. E. Dunham. 1983. On hypothesis testing in ecology and evolution. Amer. Natur. 122:602-617.
Romesburg, H.C. 1981. Wildlife science: gaining reliable knowledge. J. Wildl. Manage. 45:293-313.
        (on WyoWeb)

References for and against Bayesian approach:

Dennis, B . 1996. Discussion: Should ecologists become Bayesians? Ecol. Applic. 6: 1095-1103. [against]
Ellison, A.M. 1996. An introduction to Bayesian inference for ecological research and environmental decision-making. Ecol. Appl. 6: 1036-1046.
Hilborn, R., and M. Mangel. 1997. The Ecological Detective: Confronting Models with Data. Princeton Univ. Press.
         (search for appropriate sections)
Iversen, G.D. 1984. Bayesian Statistical Inference. Sage, Beverly Hills QA 279.5 .I94 1984.
Press, S.J. 1989. Bayesian Statistics: Principles, Models, and Applications. New York: Wiley. QA279.5.P75 1989
Reckhow, K.H. 1990. Bayesian inference in non-replicated ecological studies. Ecology 71: 2053-2059.

Other references:

Anderson, D.R., K.P. Burnham, and W.I. Thompson. 2000. Null hypothesis testing problems, prevalence, and an alternative. J. Wildl. Management 64: 912-923.
Hudson, P.J., A.P. Dobson, and D. Newborn. 1998. Prevention of population cycles by parasite removal. Science 282: 2256-2258.
Korpimaki, E., and K. Norrdahl. 1998. Experimental reduction of predators reverses the crash phase of small-rodent cycles. Ecol. 79: 2448-2455.
Marquis, R.J., and C.J. Whelan. 1994. Insectivorous birds increase plant growth through their impact on herbivore communities of white oak. Ecology 75:2007-2014.
Starfield, A.M. 1997. A pragmatic approach to modeling for wildlife management. J. Wildl. Mgmt. 61: 261-270
             (in the suggested readings folder on WyoWeb)

§§§§ §§§§§§§§§§§§§§§ §§§§§§§§§§§§§§§§§ §§§§§§§§§§§§§§§§§ § §§§§§§§§§§§§§§§ §§§§§§§§§§

Return to top of page         Go forward to notes for Lecture 4,  23-Jan