Return to Main Index page          Go to Lecture 16         Go to Lecture 17  

Go to movie of discrete logistic 2-cycle (r = 2.2) case        Go to movie of discrete logistic chaos (r = 3) case

Intraspecific competiton -- discrete logistic equation
      low r slightly oscillating approach to K case

                  Eqn 15.1

Embedded QuickTime Movie (from Mathematica notebook r1Movie.nb)

Click on the image below to start the "movie". A control bar will appear below the graph; the various buttons will allow you to stop and start it.

Fig. 1. One-dimensional "map" of the discrete logistic (Eqn 15.1, above) with r = 1.5 and K = 1,000. Note that the population converges very quickly on K. We start with an N(t) value on the X-axis, move up to the "map" (red line) to get an N(t+x) value and then take the corresponding Y-value by going over to the 1:1 black line, then again move to the red line. Tracing the map is therefore a process of going back and forth from the red map line to the black N(t+x) = N(t) 1:1 line (like a stair step -- "up, over, up, over"). Following the map this way gives us the successive population sizes over time. Note that the trajectory moves toward the stable equilibrium point (at K = 1,000).  The last few frames involve changes so small they don't show up onscreen. 

The low r value here is what permits the convergence on K.

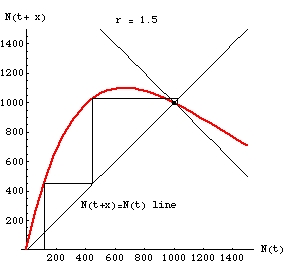
Fig. 2. Static view of the trajectory toward the stable equilibrium at K = 1,000 from a starting N₀ of 120. 
Note the stair step ascent from the starting value to K.  The very slight oscillations are shown by the lines spiralling inward around K.