Patterns of survival and mortality, part 2.

Return to Main Index page      Go back to notes for Lecture 8,  Fri 1-Feb     Go forward to notes for Lecture 10,  Wed 6-Feb

        Suggested reading: Keyfitz, Simpson's paradox (on WyoWeb)
        Handouts (on WyoWeb): demographic terms; Excel spreadsheet for life tables; xcel spreadsheet composite life table formulation for Dall sheep;
                Excel spreadsheet for µx "force of mortality

Last time I talked about broad patterns of mortality, Type I, II, and III survivorship curves, why birds and bats might have generally longer lifespans than mammals of comparable size and then ended by introducing an example of Simpson's paradox. (I have put a reading assignment from a book by Nathan Keyfitz in the WyoWeb folder).

Try another one with "political" implications. Female applicants to Berkeley were turned down at a rate considerably higher than that for men. Their test scores (GREs) were higher than the men's. Bias? Actually not; department by department, female acceptance rates were higher than those for males (in accord with their higher test scores). How can this be?

Answers:

French Canadians are a minority of the whole population and most of them live in Quebec.

Women applied to departments with lower acceptance rates.

I raised the issue of Simpson's paradox, because it applies to the problem of detecting senescence in natural populations of birds. The dogma has long been that birds have fairly constant mortality rates and do not exhibit marked senescence. Analysis of data for mammals provides the expected-from-theory pattern of senescence. Why not birds?

Simpson's paradox is a very slippery and potentially confounding problem. Heterogeneity (differences between groups or categories) can mask or confound patterns that would be apparent in a homogeneous group or category. Unless we know how/where to create categories and analyze our data we may get "patterns" or "results" at one scale that don't apply at another scale.

Let's apply Simpson's paradox to mortality. Heterogeneity can apply in two ways that could obscure underlying causes and patterns. The source of the heterogeneity could be in the population (e.g., high quality individuals vs. low quality individuals) or in the processes that act on the population (a force decreasing mortality late in life balancing one that increases it later in life).

1)  Selection through time. Worst die off first at high rate; best die off at low rate that accelerates throughout the life span. Result? An apparently flat pattern of mortality for the population as a whole. The heterogeneity here is in the "quality" of individuals. "Good" and "bad" individuals have different death rates over time. The problem is to tell the "good" from the "bad" by something other than the rate at which they die. That may often be very difficult.

2)  Conflicting processes (here the processes are the source of the heterogeneity). Two sources of mortality acting simultaneously in opposite directions might cancel each other out. A physical example of conflicting processes is the generation of two sound waves of opposite shape --the result is apparent silence. This is the basis for headphones that "cancel" airplane engine noise. We can imagine similar processes occurring with mortality. One process increasing mortality early in life (or in one possibly unrecognized, uncategorized portion of the population) and another decreases it later in life. The cancellation produces an overall pattern of no change, but within a category (just the airplane engine or just the silencer headphones), quite a lot is going on that might be of real interest.

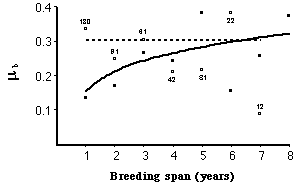
Fig. 9.1. Force of mortality, µ_x, for Florida Scrub-Jays as a function of age (measured as breeding span, meaning the number of years that an individual survived as a breeder). If we look at all the birds in the population we see no evidence of senescent mortality (dashed line, based on open circles). If, however, we look only at the subset of "high-quality" individuals then we see a clear increase (solid line, based on solid symbols). Why no overall pattern? Because the full data set includes a contingent of very "low-quality" individuals that die off quickly. The high mortality, early on, of these low-quality birds pulls up overall mortality to the dashed line.  Selection through time weeds them out and the remaining (mostly high-quality) birds have mortality that increases with age.  [From McDonald et al. 1996].

The force of mortality, µ_x, is a useful measure because, unlike age-specific survivorship (q_x), it is independent of the census interval.  This means, for example, that it permits us to compare annual survival in elephants to daily survival in fruit flies.

The Florida Scrub-Jay analysis suggests that, like other animals, birds probably do have a pattern of senescent mortality (mortality increasing with age rather than a strictly constant Type II curve).  The problem is, it is hard to know that the population consists of two different pools -- "high-quality" and "low-quality."  Using higher mortality as a basis for detecting "low-quality" won't work because it is circular logic.  For many bird populations we have no independent criterion on which to base judgment of quality (in the scrub-jays they differ in their fledging rates). 

We've seen some broad patterns in mortality/survivorship and some of the problems in detecting patterns within populations. How do we measure estimate survival mortality? First, let's make sure we remember why the subject matters. Mortality -- along with emigration -- is a major force acting to decrease population size or cause a negative growth rate.

One of the major ways to organize survival data is in what's called a life table. Three major types of life tables exist — the differences among them center on how we gather the data.

I.  Cohort or dynamic life table -- this type of life table is based on a single year class or cohort (e.g., all animals hatched or born in 1981).  We keep track of those individuals and recount them yearly, keeping track of the number of deaths.  We follow the cohort until all have died.  The cohort life table approach is generally not feasible for very longlived species.  The cohort approach does generally yield the best data, but it also makes the most assumptions (e.g., that the cohort(s) tracked accurately represents the population) and is usually the most difficult to obtain in the field.

II.  Static or time specific — data gathered during a short period of time

We take a cross section of age classes at one instant Estimate mortality by age class — estimating age specific mortality from sample of current age structure. Mortality cannot readily be inferred because present age structure may depend not only on current mortality but also on number of young produced in past years and on mortality during previous time periods.
Major assumptions

Birth rate has been constant
Mortality rate has been constant
Population is at equilibrium (stable age distribution)
We have unbiased sample of population

Go to Excel spreadsheet illustrating the difference between a cohort and static life table with a hypothetical numerical example.

III. Composite life table — uses data collected over an indefinite period (several years) involves a number of cohorts and samples a cross section of population. It combines following individuals through time with the (logistically easier) method of making inferences from the current age structure.

Composite tables most often used in wildlife because you can pool data over number of years — increase sample size & don't have to follow cohort to death. Its assumptions are more likely to be met:
Age structure constant
Population is stationary (neither growing nor shrinking)
Disadvantages: - Averaging over years masks temporal variation that may be of interest to managers.

I have placed an example of a "composite" life table for Dall sheep in an Excel spreadsheet on the WyoWeb course site (in the "Handouts" folder).  The data for this example were calculated from Dall sheep skulls collected in McKinley Park by Murie in the 1940’s. The data are neither from a single cohort nor from a single slice in time. Instead, they represent a (we hope more or less random) sample of individuals that died over a series of years.  Note that viewing the data as l_x (proportion surviving), q_x (age-specific mortality rate), and m_x (force of mortality), emphasize different aspects of the life history.  For example, all three pick up the blip of mortality at age two (when young animals become independent and vulnerable, and young males often wander widely).  q_x and m_x emphasize the jagged tail end of the curve.  This is a common feature of such data, where sample sizes get very small at advanced ages and zigzag up and down somewhat erratically.

WyoWeb folder also has a "handout" on the various l_x, q_x, d_x, and other demographic terms used in life table analyses.

An extensive literature exists for estimating survival rates, particularly from mark-recapture data.   That falls more in the province of a wildlife techniques course such as ZOO 4300.  One of the major techniques is some variant on Jolly-Seber models.  Good references include:
           Caughley, 1977
           Krebs, 1999, Ch. 14.

Caughley, G. 1977. Analysis of Vertebrate Populations. Wiley, New York.
Keyfitz, N. 1985. Applied Mathematical Demography. Springer-Verlag, NY.
Krebs, CJ. 1999. Ecological Methodology.  (Ch. 14 Estimation of survival rates). Benjamin Cummings, NY.
McDonald, D.B., J.W. Fitzpatrick, and G.E. Woolfenden. 1996. Actuarial senescence and demographic heterogeneity in the Florida scrub jay. Ecology 77: 2373-2381.

Return to top of page                    Go forward to notes for Lecture 10,  6-Feb