Lecture notes for ZOO 4400/5400 Population Ecology
Lecture 21 (Wed. 13-Mar-13) Lotka-Volterra competition equations (continued).
Return to Main Index page
Go to back to lecture 20 , Wed. 6-Mar
Go
forward
to lecture 22 of Fr. 15-Mar
Last time we used equations and graphical arguments
to explore the conditions under which the Lotka-Volterra equations
could
produce outcomes of stable coexistence and unstable coexistence.
Now we'll look at the other major possible outcome -- competitive
exclusion.
{Here we have two subcategories -- Species 1 always wins or Species 2
always
wins}.
Here's a graphical depiction of one of the two possible cases of competitive
exclusion.
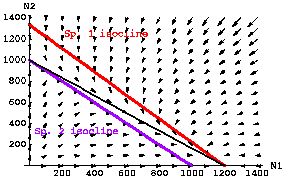
Fig. 21.1 Competitive exclusion of Species 2 by
Species 1 (Species 1 "wins"). If the isocline of one population lies
completely above the isocline of the other population, it will "win" from any
starting point at which its abundance is > 0. If the isoclines do not cross, no coexistence equilibrium exists, the
only equilibria are all Species 2 (an unstable equilibrium, because as soon as N1
>0, N1 will increase to its K1 and drive N2 locally extinct), and all
Species 1 (a stable equilibrium, because even if more N2 show up later, the trajectories will move toward their
local extinction). Here, inequalities listed in Eqns 21.1 satisfy the conditions
for a "win" by species 1.
Parameter values: r1 = r2= 0.5; K1= 1,200;
K2= 1,000; g12 = 0.9; g21 = 1.0.
Look back over Figs. 20.1 to 20.3 and Fig. 20.1. I have covered all the major possible
outcomes for our two-species logistic competition model. Let's now look at an inequality-based summary of how we can analyze the stability
properties of such models via equations and graphs.
Equation-based summary of outcomes:
Stable coexistence:
K1 / g12 > K2 and K2
/ g21 > K1
Eqns 21.1
Unstable coexistence: K1
/ g12 <
K2 and K2
/g21 < K1
Species 1 wins:
K1 / g12 > K2 and K2
/g21 < K1
Species 2 wins:
K1 / g12 < K2 and K2
/g21 > K1
Note that the inequalities above differ in that each has a different
combination of > (greater than) and < (less than) signs.
The terms (which represent the X- and Y-intercepts for the isoclines)
are exactly the same throughout. That is, they make statements
about the order in which the isoclines hit the N1 and N2 axes.
Again, these equations set the conditions for the three major outcomes,
but it is generally much easier to use graphs to determine outcomes.
Likewise, it is usually much easier to look at "maps" of
dispersion
to decide whether a population is clumped, randomly distributed or
uniformly
distributed than it is to use analysis of counts per quadrat and the
fit
of the data to a Poisson distribution. Nevertheless, the counts
(frequencies,
means and variances) are useful for quantifying the degree of
clumping
or uniformity, and for deciding whether a roughly random pattern is
somewhat
clumped or somewhat uniform. ____________________________________________________________________________________________________
How can we tell which outcome will occur, just by looking at the graphs?
IF the isoclines cross in
such a way that the "visitor's" isocline hits the "home" species' axis above
the "home team's" isocline, the coexistence is stable.
(Or, equivalently, if the isoclines are straight lines and cross above
the K-connector, then we have the stable case).
IF the isoclines cross in such
a way that the "visitor's" isocline hits the "home" species axis below
the "home team's" isocline, the coexistence is unstable. (Or,
equivalently, if the isoclines are straight lines and cross below
the K-connector, then we have the unstable case).
IF the isoclines don't cross each other then
whichever species has its isocline on top will outcompete the other species
and drive it to (local) extinction. (Or equivalently, if the K-connector
is between the isoclines and they do not cross it, then we have the competitive
exclusion case). [If most of the parameters (ri
and Ki) are equal, it will tend to be the case that gi > 1 will give Species j an edge and lead to competitive
exclusion of Species i (but see below)].
OR... the vector-sum
method (probably best of all)
use the trajectory/vector method.
Above the N1
isocline, N1
will be declining (leftward arrow). Below its own isocline N1
will be increasing. Above the N2
isocline, N2
will be declining (downward arrow). Below the N2
isocline, N2
will be increasing (upward arrow). IF the isoclines cross, they
create
four "regions":
1) Above both isoclines (leftward plus downward
vectors
yield a sum vector pointing SW);
2) above the N1
isocline but below the N2
isocline
(leftward plus upward vectors yield a sum vector pointing NW);
3) below N1
isocline but above N2
isocline (rightward plus downward vectors yield a sum vector pointing SE);
4) below both isoclines (rightward plus upward vectors yield a sum vector pointing NE).
Several good points about the vector sum technique:
a) It is quite general. It also works well for graphical analysis of predator-prey equations
and other paired equation analyses.
b) All you need to know to get started is
i) which isocline is which (a species own
isocline
goes to its K on its axis),
ii) that a species declines above its isocline and
increases above it.
_____________________________________________________________________________________________________
Some twists (potential pitfalls) in the Lotka-Volterra approach:
Stable coexistence case:
I. Stable coexistence but below K-connector:
the effect of curved isoclines
Ayala et al. (1973) ran some interspecific competition
experiments and had a puzzling outcome. They found stable coexistence in some cases where the equilibrium point (intersection of the
isoclines) fell below the K-connector.
Puzzling data:
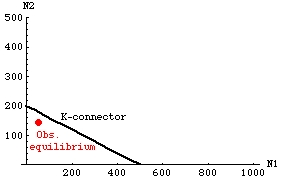
Fig. 21.2. Observed stable equilibrium numbers of two species of Drosophila following a competition experiment. Note
that the combined population point (equilibrium) lies below the K-connector.
At first this seemed impossible, given the inequalities of Eqns 21.1. The stable coexistence outcome should have an equilibrium above
the K-connector (see above). They carefully
checked their empirically calculated estimates of K, and found that
they were repeatable and precise. What they finally realized was that they had made an assumption of linearity for the isoclines -- the
factors allowed by the model led inevitably to linear isoclines.
Perhaps, the conclusion that "if the isoclines intersect below the K-connector,
the coexistence is unstable" rule (see above) was simply an artifact of the model assumptions.
If the isoclines are linear and they cross above the K-connector, then yes, we have the stable equilibrium case. BUT, the
isoclines can cross below the K-connector, and coexistence can still be stable,
IF the isoclines are curved, as in the graph below. A slightly
more complex model can produce curved isoclines, and curved isoclines are
consistent with the observed isoclines. When they monitored the population
trajectories through time, those too were more consistent with a curved-isocline model than with the simpler linear model.
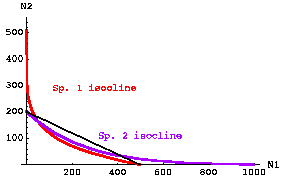
Fig. 21.3. Stable coexistence with curved isoclines. Note
that the isoclines cross below the K-connector. Nevertheless the intercepts satisfy the inequalities of Eqns 21.1 for stable
coexistence -- that is, the "visitor" isoclines reach the intercept further out
than the "home" isocline on both axes. This modification of the original
linear Lotka-Volterra theory (via slightly more complex equations 21.2 and 21.3) was developed to provide an explanation for experimental results with Drosophila.
Note that the vector sum method can accommodate this sort of change in the assumptions. Try dividing a sketch of curved
isoclines into four areas and putting one arrow in each zone --
1) Above both isoclines (arrow points SW). Both species decrease (toward equilibrium point).
2) Above Sp. 2 isocline, but below Sp. 1 isocline (the small area between the isoclines at values of N2 between 200 and 300,
near the N2 axis). Arrow points SE toward equilibrium intersection of the two isoclines.
3) Above Sp. 1 isocline but below Sp. 2 isocline (long, very narrow area between the isoclines at values of N1 between
500 and 800, near the N1 axis). Arrow points NW toward equilibrium intersection of the two isoclines.
4) Below both isoclines (arrow points NE). Both species increase (toward equilibrium point).
The model represented by Eqns 21.2 and 21.3 and Fig. 21.3 uses just a few additional assumptions and mathematical terms to allow us to fit
a (relatively) simple model to real-world data.
For the interested (small blue font material): The curved isoclines result from using
modifications of Eqns 20.1 and 20.2 with power terms:
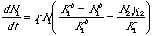 Eqn 21.2
Eqn 21.2
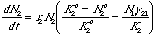 Eqn 21.3
Eqn 21.3
All we have done
to change Eqns 20.1 and 20.2 is to add power terms to the "home" species terms inside the bracket. The power terms make the isoclines
nonlinear.
II. Stable coexistence with gammas unequal and one of them > 1.0: Note that we can have a
stable coexistence case even if one of the gij > 1.0. That is, what matter for coexistence are the inequalities
given by Eqns 21.1. [Try these values to see a stable case with a g > 1]. Parameters: r1 = 0.3; r2 = 0.5, K1
= 1,400, K2 = 1,000, g12 = 1.1,
g21 = 0.6].
Unstable coexistence case:
Parameters exactly equal, equal populations sizes (unstable equilibrium): Note that we can move along a
very limited set of trajectories toward unstable coexistence under certain (very unrealistic) conditions. If the two species have all parameter
values the same AND the population sizes are equal, they will move toward the intersection of the two isoclines and then have no tendency to move
away. As soon as one or the other gains a numerical advantage, though, it will move toward its carrying capacity while driving the other to (local)
extinction. Even if we start with N1 > N2 by just
one animal, N1 will "win". Conversely, if we start with N2 > N1 by just
one animal, N2 will "win". Any starting points that are not along that line will
not move to the equilibrium point but will curve toward the "winner's" axis.
[We could also create such linear trajectories in the more complicated case that the parameter values were not exactly
equal. The result would still be a line going diagonally through the equilibrium point].
References:
Ayala, F.J., M.E. Gilpin, and J.G. Ehrenfeld. 1973. Competition between
species: theoretical models and experimental tests.
Theor. Pop. Biol. 4: 331-356.
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Return to top of page
Go forward to lecture 22 of Fr. 15-Mar



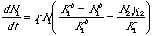 Eqn 21.2
Eqn 21.2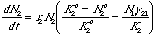 Eqn 21.3
Eqn 21.3