Civil and Architectural Engineering and Construction Management
EN 3074
Dept. 3295
1000 E. University Ave.
Laramie, WY 82071
Phone: (307)766-2390
Email: cae.info@uwyo.edu
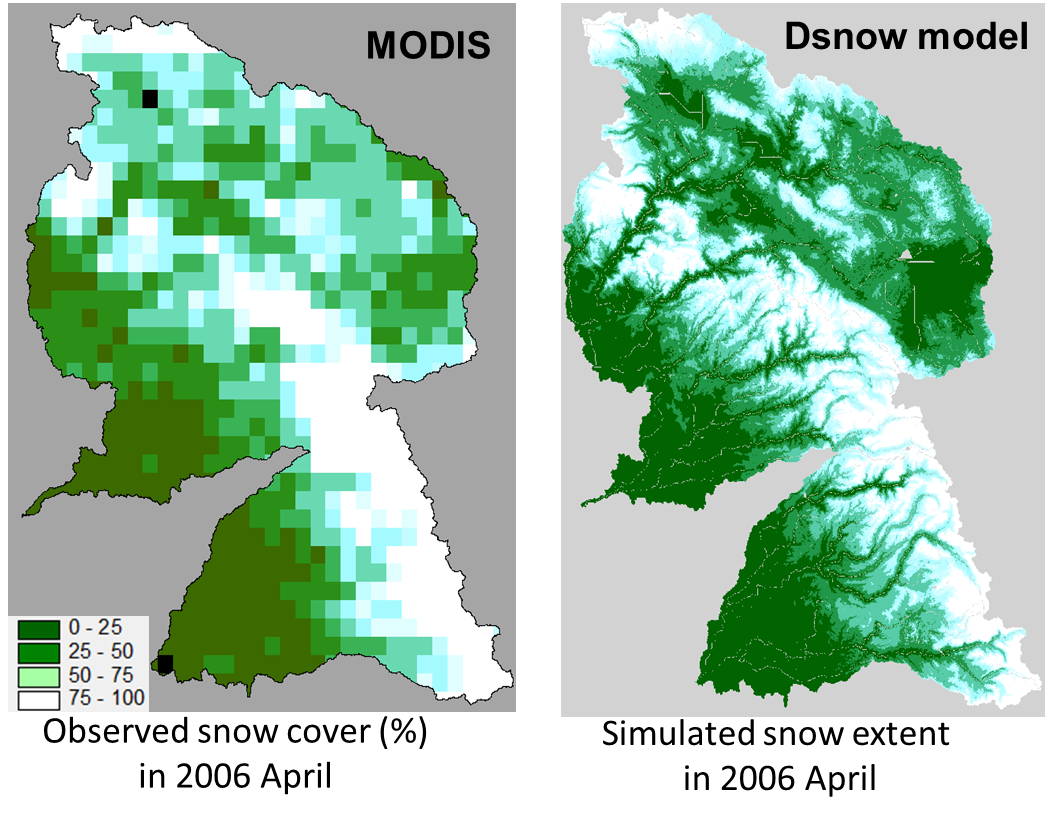
Distributed snow modeling with topography and canopy effect
We have developed a snow energy balance algorithm that can compute the snow state
very efficiently for distributed model. This spatially distributed snow model was
named as Dsnow model. This snow model explicitly incorporates the vegetation cover
effect on snowmelt process. An example model output in the Feather, Yuba, American
River watersheds, CA, the US, was visualized in left figure. More applications of
this model can be found in the publications: Ohara and Kavvas (2006), Chen et al.
(2011a), Ohara et al. (2013).
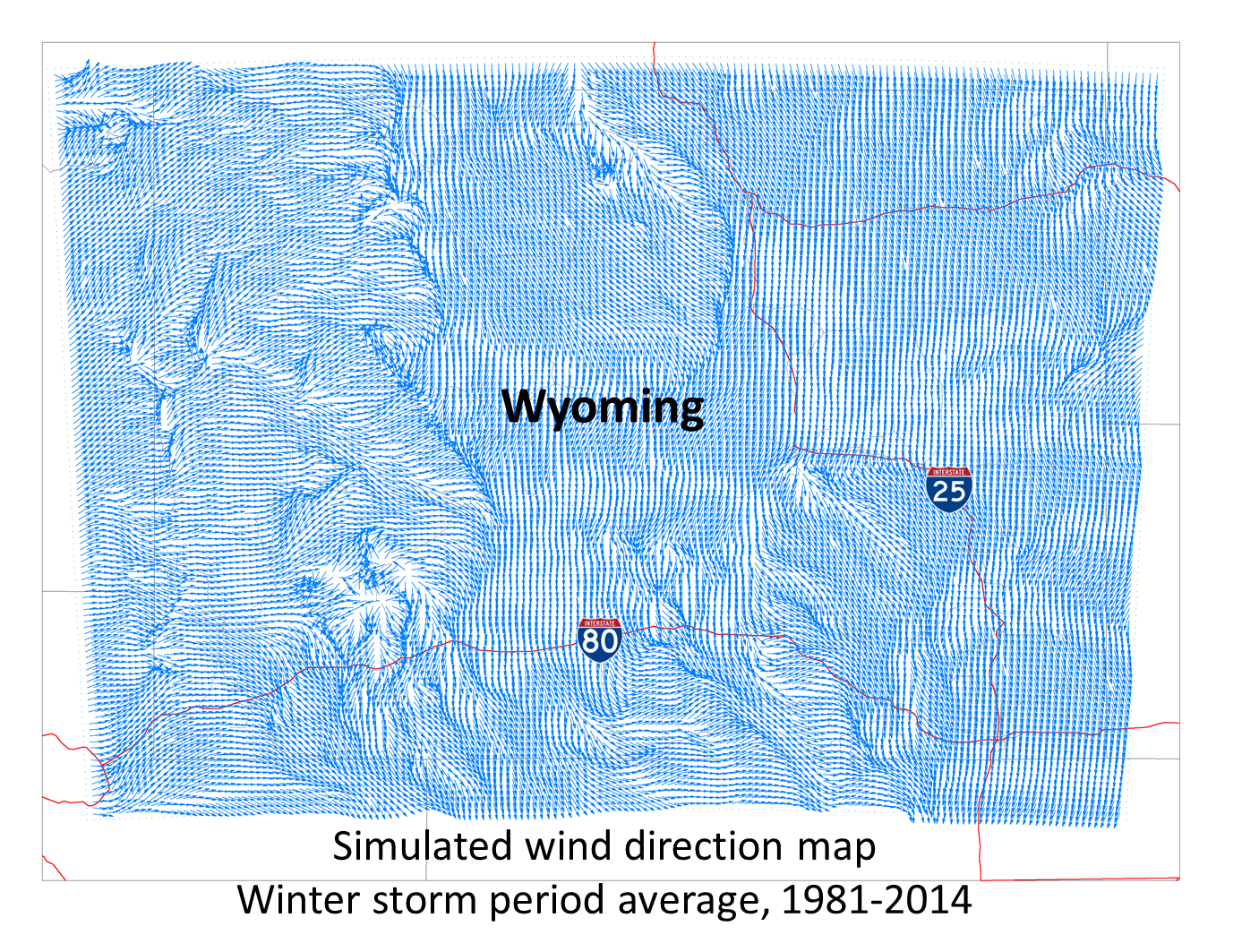
Numerical weather model for atmospheric forcing
The dynamic downscaling technique using a numerical weather prediction (NWP) model
can effectively meet the data requirements of the process-based snow model even in
ungauged or sparsely gauged basin. The NWP model can also quantify the historical
wind and snowfall field in Wyoming for better snow fence system design. The simulated
historical wind field is shown in right graphic. The numerical weather model was used
for physically-based probable maximum precipitation (PMP) estimates (Ohara et al.
2011). One of series papers on this topic, Ishida et al. (2015), was awarded the American
Society of Civil Engineers (ASCE) J. James R. Cross Medal 2016, the second highest
research paper award in the ASCE.
Field study of snowmelt runoff process
Ohara et al. (2012) performed a field study at the northwest sector of the Ward Creek
watershed, Lake Tahoe Basin. They observed the significant overland/in-snow flow even
over the unfrozen unsaturated topsoil of a snow-covered hillslope. This overland/insnow
flow that can amplify the peak flow discharge may be a more common phenomenon than
has been considered on a snow-covered hillslope. This finding was verified by another
field experiment in Snowy Range, Wyoming.
Snow redistribution modeling
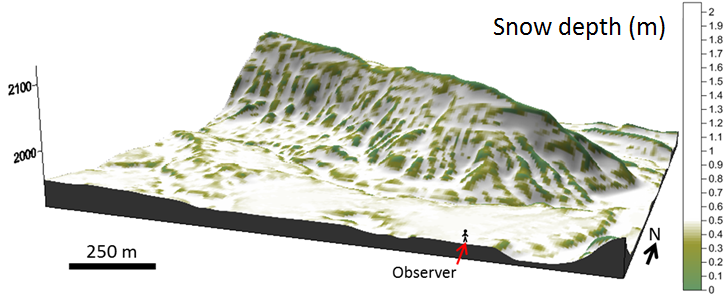Ohara et al. (2014) generalized the snow movement equation for watershed scale applications
by incorporating snow transport, wind snow diffusion, and snow gravitational movement.
This new formulation can explicitly describe the snow diffusion process by wind turbulence.
The proposed formulation was tested through the model simulation using a 10-m digital
elevation model in Muddy Gap, Wyoming, as shown right. We try to understand the blowing
snow processes using the theoretical and field approaches.
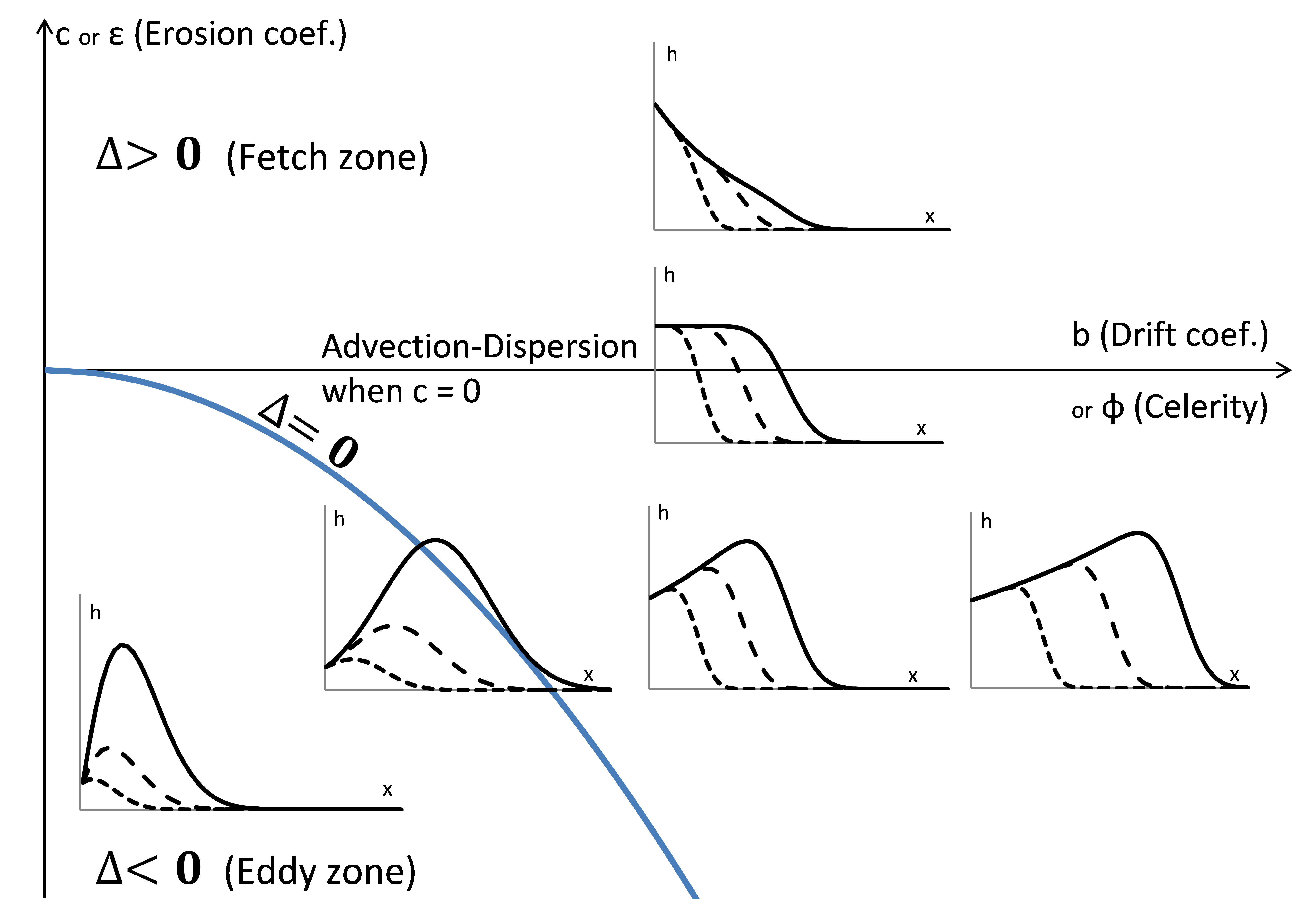
Snow drift prediction
Snowdrift process was formulated as a linear partial differential equation based
on Eulerian framework (Ohara, 2017). Ohara (2017) showed that most of the particle
deposit patterns behind an object can be characterized by the particle motion parameters:
diffusion, drift, and erosion coefficients (schematic right, from Ohara 2017). This
new formulation can improve understanding of particle distribution patterns found
in the fields of riverbed erosion, sedimentology, aeolian landforms (e.g. ripples
and dunes), as well as snowdrift.
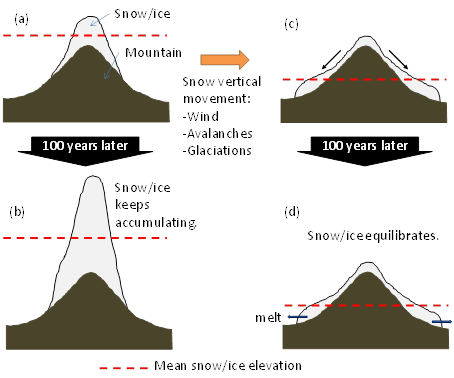
Inter-annual snow modeling
Energy and mass balance model for terrestrial ice and snow is the most powerful tool
for future projection of inter-annual snow storage. However, the snow models in hydrologic
engineering field cannot handle the long-term snow storage due to lack of snow movement
parameterization (schematic left, from Ohara et al. 2014). We have been working on
an appropriate treatment for inter-annual snow including inland glaciers as systems
in dynamic equilibrium that stay constant under a static climate condition.
Civil and Architectural Engineering and Construction Management
EN 3074
Dept. 3295
1000 E. University Ave.
Laramie, WY 82071
Phone: (307)766-2390
Email: cae.info@uwyo.edu
