NMR Basics
This facility is a shared resource serving the University of Wyoming community and beyond. It currently houses six NMR spectrometers that are used for a multitude of research in science, engineering, and teaching. The purpose of this page is to give the reader some background information about what this facility is doing and why it is so useful for many people and how it could be more useful for non-users if they only knew how much they have been missing so far.
It is hoped that this presentation of the basics of NMR spectroscopy is more accessible than the commonly found one in textbooks or websites.
Almost all samples give a NMR spectrum
This facility deals with magnetic resonance, in particular nuclear magnetic resonance. It gives data from a sample that is subjected to a magnetic field and certain resonance conditions. The sample can be of any kind, it could be liquid, solid, or even gas. The sample will be affected by the magnetic field as long as it contains either protons, neutrons, or electrons, or any combination of them, so just about any sample. If these "magnetized" protons, neutrons, or electron can be cleverly brought into "resonance", the result is "Nuclear Magnetic Resonance" if the nuclei composed of protons and neutrons are brought into resonance, "Neutron Magnetic Resonance" for neutrons in resonance, and "Electron Spin Resonance" for electrons in resonance. This facility deals with nuclei in resonance: Nuclear Magnetic Resonance, or abbreviated NMR. In practical terms, almost any chemical element has a nuclear isotope that is NMR active. This makes NMR spectroscopy especially interesting for chemists.
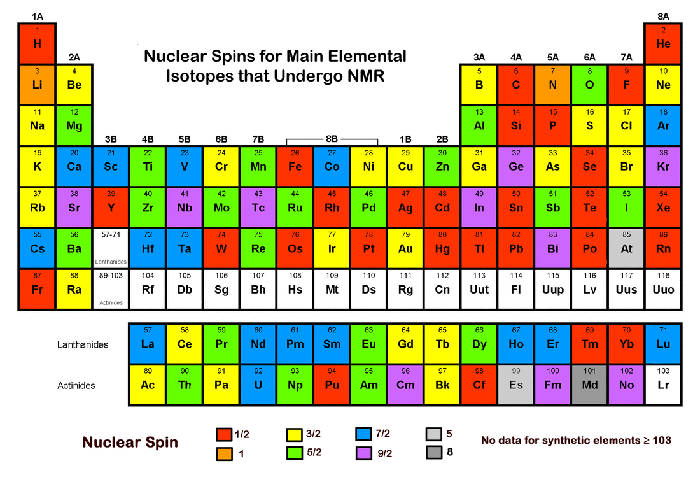
Magnetic fields can influence "spins" that can be brought into "resonance"
Historically, all three phenomena, Nuclear Magnetic Resonance, Electron Spin Resonance, and Neutron Magnetic Resonance, have been known for more than 60 years, all since about a 10 year window around the end of World War II (1945). They all rely on a property of nuclei, protons, neutrons, and electrons to possess a "spin". However, it should be emphasized that this "spin" ought not be imagined as something that physically spins like to top, a children's toy. Rather, this is merely a classical description of a quantum number as something that a physical entity just happens to possess (there is no classical analogue). A similar misleading description of the constituents of protons, electrons, muons, the color of the quarks, has likewise no classical analog. Nobody has seen a "color" of quarks, nor nuclei spinning. In spite of this, most descriptions of magnetic resonance rely on pictures that show something spinning in the hope that this helps to understand the concepts. Quantum-mechanical density matrix descriptions may be overkill for many people who just want to run a spectrum, or so it goes. Anyway, it might be more fun to illustrate magnetic resonance with spins as it allows some artistic freedom that may make the concept more visually appealing (see following picture).
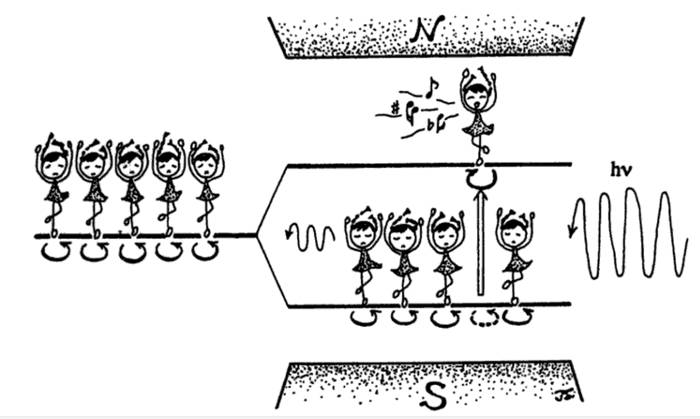
This pictures describes a sample with magnetizable properties ("spins") that is brought into a magnet. The magnet splits the energy levels and the resonance condition, an electromagnetic wave, perpendicular to the magnetic field, of a suitable frequency that exactly matches the energy difference between these levels, induces transitions between these levels and emits a response ("music"). That's the basic concept of magnetic resonance.
Stronger magnetic fields improve sensitivity and resolution
The splitting of the energy levels depends on the magnetic field. In the following picture, 2 million "spins" have been subjected to a magnetic field of different strength. In reality, a sample usually contains an amount of spin in the neighborhood of (1x10-3)x(650x10-6) x ( Avogadro's number (~6 x 1023)) ~ 4x1017, for 650 ul of a 1 mM sample, so many times more than 2 million.
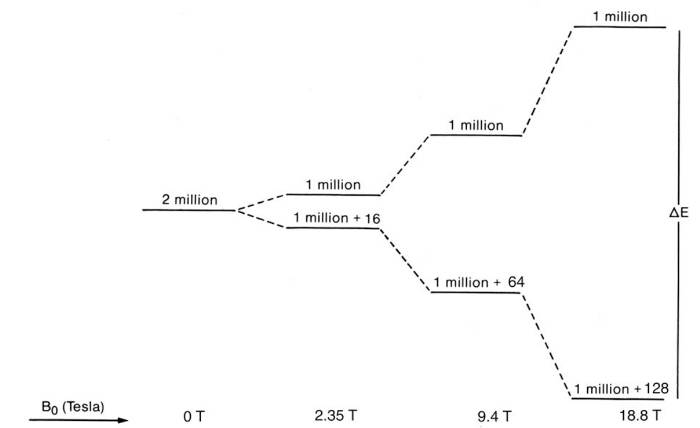
Two things are happening when the magnetic field increases. It increases the energy gap between the levels, and it also increases the population difference of the levels. That basically means the signal to noise ratio goes up as the magnetic field increases. An increase in the energy gap can distinguish the initial energy levels better, so it increases the spectral resolution. The sample itself has internal magnetic fields that arise because of the presence of different nuclei and electrons and bonds within the sample. So now it becomes apparent how NMR can help in chemistry. It can decipher these energy difference within the sample, thus can find the atomic structure of substances. But that is not all. In all samples, the samples are not static, but the constituent parts such as molecules move because of temperature, they may have different phases (solid, liquid, gas) and that can be seen in appropriate NMR measurements.
The figure above essentially comes from the Boltzmann equation where the population ratio between the upper and lower energy states is just = exp (- (energy difference)/kT))
To put the strength of the magnetic field in context, the earth's magnetic field strength ranges from 0.00025 - 0.00065 T (25 to 65 microTesla). The "60 MHz" magnets employ a field of 1.41 T, and the "600 MHz" magnets employ a field of 14.1 T, so the dependence of the energy difference on the magnetic field strength is linear. Permanent magnets are difficult to construct for more than 2 T, and superconducting magnets are commonly used. Superconducting magnets are cooled by liquid helium and usually insulated by another layer of liquid nitrogen. Incidentally, the MHz rating of NMR magnets refers to the resonance frequency of protons in that magnetic field. While it is possible to use the earth's magnetic field to do NMR, the sensitivity is extremely low. That's why there is a drive to use stronger and stronger magnetic fields. The spectral resolution also increases with increasing magnetic fields. Although many regard "bigger" as "better", this is not necessarily the case. Very strong magnetic fields also tend to simplify the spectra that make them easier to interpret and quicker to acquire, but also there is some loss of information. Sometimes it is desirable to make NMR measurements at different magnetic field strengths, for example, for spectral assignments (see below) or dynamics studies as the relaxation (see below) depends on the magnetic field strength.
Free induction decays (FIDs) and NMR spectra
There are two main ways to achieve magnetic resonance. Either by changing the magnetic
field B, H or by changing the incident waves hv, or both. Many versions have been
tried in the past, but few people will encounter any NMR spectrometer whose main magnetic
field strength is not constant these days. This has to do with the prevalent use of
superconducting magnets and the ease of changing the incident waves hv in complex
ways, that effectively not only have a single wavelength but cover a whole spectrum
simultaneously. That is the birth of Fourier transform NMR. Virtually all current
NMR spectrometers are Fourier-transform NMR spectrometers. They rely on the incidence
of complex waves, so called pulses, that consist of a broadband of different frequencies
that excite nuclei in many different environments. Not surprisingly, the output, the
response is also a complex wave, the so called FID (free induction decay). A simple
case is depicted below. It may come from just a liquid sample of water in which the
hydrogen atoms give rise to the FID and the NMR spectrum.
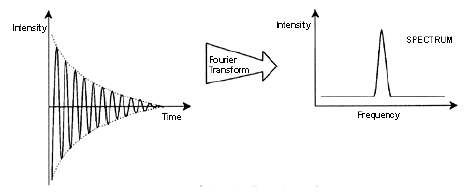
The FID decays with time (related to relaxation). A mathematic operation called Fourier
transformation converts the FID, a function of intensity and time, to a NMR spectrum,
a function of intensity and frequency. More complex FIDs and their corresponding Fourier
transforms are shown in the next picture:

The top shows a NMR spectra of one "spin", the middle of two "spins" that do not interact
with each other, while the bottom shows more than two "spins" that interact with each
other. So the FID and spectra can show many "spins" and their interactions at the
same time.
Interpretation of NMR spectra
Every sample has a unique NMR spectra. NMR data consist of a graph of amplitude as a function of frequency. As mentioned above, the frequency depends on the strength of the magnetic field. In order to better compare NMR spectra collected at different field strength, it has become custom to convert frequency to a dimensionless quantity called chemical shift with unit ppm (parts per million).
The chemical shift relates to differences in frequencies:
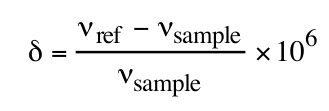
as a function of the sample frequency (vsample) and the reference frequency (vref).
The chemical shift (relative to a standard or reference) gives information about the chemical environment of the nucleus that gives rise to a peak at a particular chemical shift. The intensity (area) is proportional to the amount of nuclei in the same chemical environment (that makes it easy to deduce how many protons, for example, are attached to a particular side group). Typical ranges in chemical shifts are in the ppm range (parts per million) and are about 15 ppm for 1H, 250 ppm for 13C, 400 ppm for 15N, and 35 ppm for 31P.
Usually the NMR spectrum shows more signals than different nuclei in the sample due to line splitting and couplings between the nuclei. The amount of splitting (number of lines) and magnitude of the coupling constant depend on the number of magnetically equivalent spins and the distance between the spins. The job of the NMR spectroscopist is to decipher these couplings and assign each signal. Spectroscopists usually extract the following information from NMR spectra:
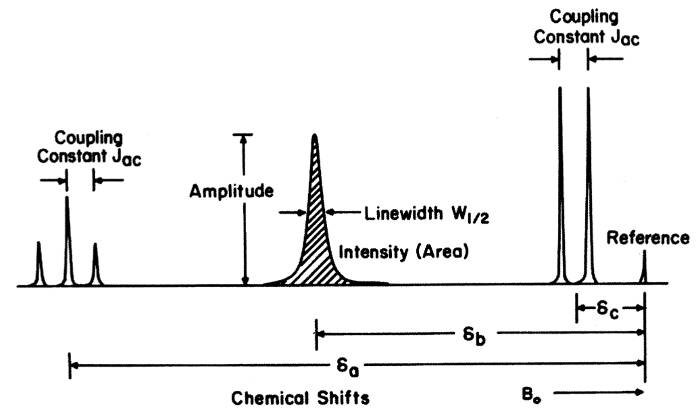
Chemical shift values, coupling constants, areas are extracted for each spin system, i.e., a collection of signals that came from a particular nucleus in a particular chemical environment. Repeating this procedure for all signals in the NMR spectra gives information about the chemical composition of the sample and also dynamics such as motion and interaction between different chemicals in the samples. Spectral libraries are available. Often NMR spectroscopy is used for determining the content and purity of a sample. The NMR spectra of a sample are not the same at different magnetic field strengths. Especially below 200 MHz, the spectra are often very complex because the separation of resonance frequencies of the nuclei are no longer small compared to coupling strengths. Above 300 MHz these effects are often absent (high field NMR). Trained NMR spectroscopists can interpret a NMR spectrum in a few seconds for simple molecules.
Advanced NMR spectroscopy
As the relaxation time in NMR spectroscopy is relatively long (~ seconds) and the pulse durations relatively short (~ microseconds), the sample "remembers" any incident pulse for long enough to be able to subject it to additional pulse without it "forgetting" the previous pulses. Thus, it is possible to put many different pulses into the samples at different time intervals to carefully manipulate the magnetization of the sample ("spin acrobatics"). This can help to measure complex interactions between thousands of nuclei that are commonly found in biological macromolecules such as proteins. In biomolecular NMR spectroscopy, the pulse trains are very complex and give rise to multidimensional NMR. The interpretation of these spectra can take months.
Some mathematics.
The mathematics of describing magnetic resonance is very complex and few people ever attempt to describe the phenomena accurately and in detail. That is regrettable, but results in the observation that few physicists remain in the field, although the field was initially dominated by physicists. NMR is inherently a quantum phenomenon that cannot be explained classically. It a quantum-based effect of the interactions between magnetic and electric fields, that is a relativistic/quantum extension of the Maxwell equations, such as quantum field theory, and that needs to be considered for even the most basic interpretation.
To give some idea how to approach the problem, the problem is to find the solution of the Hamiltonian of the system (whose eigenstates in the wavefunction basis are the allowed energies):
H = βNI⋅gN⋅H + βS⋅g⋅H + Hel + HCF + λL⋅S + HSS + ∑S⋅A⋅I + HH + HQ
The terms describe the interaction of the magnetic field H with nuclei spins I and
electronic spins S, with each other, and within the substance that also takes electric
fields into account. These terms are what most people are interested in, although
the physical terms may be unfamiliar for many users. They shift the energy levels
such that every sample has a unique NMR spectrum.
Many quantities are tensors. That makes solid-state NMR so difficult to interpret and solid-state NMR experiments difficult to run. In liquids, due to rapid motion a lot of the effects average out. That may result in a loss of information, but more often gains information due to less spectral overlap in non-crystalline samples. Caution is advised, however, if the sample temperature is lowered below the freezing point in "liquid" state NMR experiments as the resulting spectra look quite different.
Rather than solving this equation, most people are just content that NMR spectroscopy provides useful insights into their sample, taking shortcuts in the theory whenever possible. In effect, perturbation theory is used and most terms neglected. That is not always desirable as NMR spectroscopy is much more information rich than they could imagine.
To solve the Hamiltonian, it is necessary to find the eigenvalues of the Hamiltonian. In the simplest case, such as for a nucleus of spin 1/2 in a static magnetic field (Zeeman effect):
E = ± ½gNβNH =>
ΔE = gNβNH
If the nuclei are subjected to a field of energy hv, perpendicular to H, then absorption occurs:
ΔE = gNβNH = hν
So the energy separation linearly depends on the (static) magnetic field, as already
mentioned above. At the same time as the incoming radiation induces nuclei in the
lower level to absorb energy to the higher, it also induces nuclei which are already
in the higher level to fall down to the lower level, and thus emit an additional quantum
of electromagnetic radiation (stimulated emission). The coefficients of absorption
and stimulated emission are equal. That means that if there were equal numbers of
nuclei in the two energy levels, then there would be just as many nuclei in the two
energy levels, then there would be just as many nuclei being driven down and emitting
radiation as there being driven up and absorbing radiation, there would be no net
absorption. Most normal systems obey a Maxwell-Boltzmann form of statistics, so initially
absorption would occur. But with time, nuclei driven up must be brought back to the
lower level. otherwise absorption would cease when both levels become equally population.
These relaxation processes heavily depend on the environment of the nuclei. To model
such a system, the location of all particles in the system should be known not only
at one instant in time, but for all times. Or, to keep it in the language of perturbation
theory, a series on tensor fields should be calculated.
References
Parella T. eNMR: NMR Periodic Table. Bruker, 2000
James TL. Fundamentals of NMR. Nuclear Magnetic Resonance. Bethesda: Biophysical Society. Ch 1. 1998; 1-31.
Ikeya, M. New Applications of Electron Spin Resonance. Dating, Dosimetry and Microscopy. World Scientific Press, 1993
Page created by Alexander Goroncy.

